Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.9 - Ex. 51
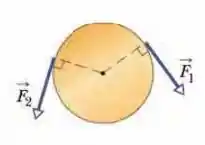
Na figura abaixo, mostra um disco homogêneo que pode girar em torno do centro como um carrossel. O disco tem um raio de 2,00 cm e uma massa de 20,0 g e está inicialmente em repouso. A partir do instante t=0, duas forcas devem ser aplicadas tangencialmente à borda do disco, como mostrado na figura, para que, o instante t=1,25 s, o disco tenha uma velocidade angular de 250 rad/s no sentido anti-horário. A força tem um módulo de 0,100N. Qual o módulo de ?
Passo 1
Show de bolinhas galerinha, pra começar, sabemos que o torque resultante sobre o disco vai ser a soma dos torque que cada força exerce, como o sentido anti-horário é o positivo, vamos ter que:
Esse torque resultante, vai fornecer uma aceleração para o disco, de maneira que:
Onde é o raio e é o momento de inércia do disco, dado como:
Logo:
Passo 2
Mas antes de substituir os valores, precisamos descobrir quanto vale , pra isso podemos usar a equação da velocidade para o movimento circular:
Como o disco parte do repouso, temos:
Logo:
Sendo assim:
Agora que já temos tudo, basta substituir os valores dados pelo enunciado:
