Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.2 - Ex. 12
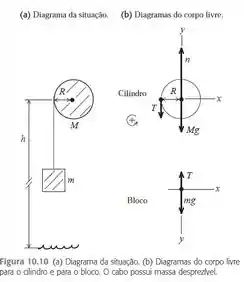
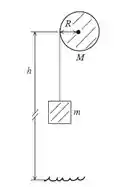
Uma pedra é suspensa pela extremidade livre de um cabo que está enrolado na periferia externa de uma polia, de modo semelhante ao indicado na Figura 10.10. A polia é um disco uniforme com massa de 10,0 kg e raio de 50,0 cm, que gira sobre mancais com atrito desprezível. Você mede que a pedra se desloca 12,6 m nos primeiros 3,0 s a partir do repouso. Ache a) a massa da pedra e b) a tensão no cabo.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que uma pedra é suspensa pela extremidade livre de um cabo que está enrolado na periferia externa de uma polia, de modo semelhante ao indicado na figura abaixo:
Queremos encontrar a massa da pedra e a tensão do cabo dado que:
- A polia é um disco uniforme com massa de e raio de , que gira sobre mancais com atrito desprezível;
- Você mede que a pedra se desloca nos primeiros a partir do repouso.
Para isso, nós vamos aplicar a segunda lei de Newton:
Onde é a força, é a aceleração e é a massa.
E a equação do torque para a polia:
Onde é o torque, é o momento de inércia e é a aceleração angular.
Para o movimento da pedra, vamos tomar como para baixo.
E a polia tem o seguinte momento de inércia:
Agora bora aplicar!! 😉
Passo 2
Aplicando as equações da aceleração constante para a pedra, usaremos:
Temos que:
Isso implica que:
Passo 3
Aplicando a segunda lei de Newton na pedra. Temos que no :
Passo 4
Somente a força de tensão possui torque em relação ao eixo que passa pelo centro de massa, de modo que a equação para o movimento de rotação em torno desse eixo é . Então, aplicando torque, temos que:
Passo 5
- A combinação dessas duas equações para eliminar T dá origem a:
Passo 6
Agora que encontramos , podemos calcular