Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.2 - Ex. 16

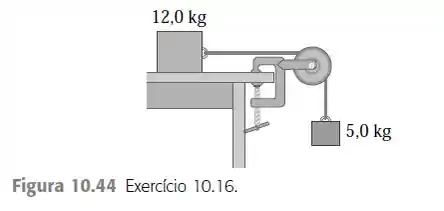
Uma caixa de 12,0 kg em repouso sobre uma superfície horizontal e livre de atrito está atada a um peso de 5,0 kg por uma cabo delgado e leve que passa sobre uma polia com atrito desprezível (Figura 10.44). A polia possui a forma de um disco maciço e uniforme com massa de 2,0 kg e diâmetro de 0,500 m. Após o sistema ser libertado, ache a) a tensão no cabo sobre ambos os lados da polia, b) a aceleração da caixa e c) os componentes horizontal e vertical da força que o eixo exerce sobre a polia.

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que uma caixa de 12,0   k g em repouso sobre uma superfície horizontal e livre de atrito está atada a um peso de 5,0   k g por uma cabo delgado e leve que passa sobre uma polia com atrito desprezível.

A polia possui a forma de um disco maciço e uniforme com massa de 2,0   k g e diâmetro de 0,500   m .

Queremos encontrar, após o sistema ser libertado, a) a tensão no cabo sobre ambos os lados da polia, b) a aceleração da caixa e c) os componentes horizontal e vertical da força que o eixo exerce sobre a polia.

Para isso, temos que lembrar que a magnitude a   da aceleração de cada caixa está relacionada à magnitude da aceleração angular α   da polia por a = R α .

Além disso, nós vamos aplicar a segunda lei de Newton para o sistema, ou seja:

F = m a

Onde F é a força, m é a massa e a é a aceleração.

E aplicar a forma análoga da segunda lei de Newton para a rotação da polia, ou seja:

τ = I α

Onde τ é o torque, I é o momento de inércia e α é a aceleração angular.

Agora bora lá!! 😉

Passo 2

Mas primeiro de tudo, vamos esboçar um diagrama de corpo livre para cada objeto:

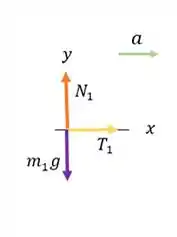
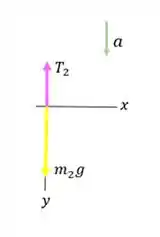
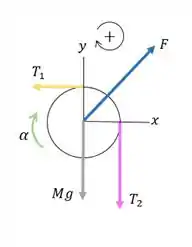
T 1 e T 2 são as tensões no fio de ambos os lados da polia.

F →   é a força que o eixo exerce sobre a polia.

E vamos tomar a rotação no sentido horário como positiva.

O momento de inercia da polia é dado por: I = M R 2 2 .

Temos os seguintes dados: m a s s a   d a   p o l i a = M = 2 k g m a s s a   d o   b l o c o   s o b r e   a   m e s a = m 1 = 12 k g m a s s a   d o   b l o c o   s u s p e n s o = m 2 = 5 k g

També sabemos que: R = 0,250 m

Passo 3

  1. Agora, podemos aplicar a segunda lei de Newton para a caixa m 1 = 12 k g :

    2. No e i x o   x :

    ∑ F x = m a x

    T 1 = m 1 a

    E na caixa m 2 = 5 k g :

    No e i x o   y :

    ∑ F y = m a y

    m 2 g - T 2 = m 2 a

    E então, aplicando para a polia: ∑ τ = I α

    T 2 - T 1 R = 1 2 M R 2 α

    Com a = R α   ficamos com:

    T 2 - T 1 = 1 2 M a

    Passo 4

    E então, adicionando estas três equações, ficamos com:

    m 2 g = m 1 + m 2 + 1 2 M a

    ⇒ a = m 2 m 1 + m 2 + 1 2 M g = 5 k g 12 k g + 5 k g + 1 k g ⋅ 9,8 m / s 2 = 2,72 m / s 2

    Passo 5

    E então, voltando para as duas primeiras equações, temos que:

    T 1 = m 1 a = 12 k g ⋅ 2,72 m / s 2 = 32,6 N

    E que:

    m 2 g - T 2 = m 2 a

    ⇒ T 2 = m 2 g - a = 5 k g ⋅ ( 9,8 m / s 2 - 2,72 m / s 2 ) = 35,4 N

    A tensão à esquerda da polia é de T 1 = 32,6 N e abaixo da polia é de T 2 = 35,4 N .

    Passo 6

  2. Nós já calculamos a aceleração da caixa no item (a), e obtivemos que:

    3. a = 2,72 m / s 2

    Passo 7

  3. Agora, nós precisamos aplicar a segunda lei de Newton sobre a polia:

No e i x o   x :

∑ F x = m a x

F x = T 1 = 32,6 N

E

No e i x o   y :

∑ F y = m a y

F y = M g + T 2 = 2 k g ⋅ 9,8 m / s 2 + 35,4 N = 55 N

Resposta

  1. A tensão à esquerda da polia é de T 1 = 32,6 N e abaixo da polia é de T 2 = 35,4 N .
  2. a = 2,72 m / s 2
  3. F x = T 1 = 32,6 N e F y = 55 N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Figura P10.82 mostra uma força vertical aplicada tangencialmente a um cilindro uniforme de peso F g . O coeficiente de atrito estático ente o cilindro e todas as superfícies é 0,500 . A força P → é
Uma bobina oca, cilíndrica e uniforme tem raio interno R / 2 , raio externo R e massa M (Fig. P10.70). Ela é montada de modo a girar em um eixo horizontal fixo. Um contrapeso de massam é conectado à p
Quando uma pessoa fica na ponta de um pé (uma posição difícil), a posição do pé é como mostrada na Figura P10.69a. A força gravitacional total F → g no corpo é suportada pela força normal n → exercida
Os ponteiros de horas e de minutos do Big Ben, o relógio da torre do Parlamento em Londres, têm 2,70m e 4,50m de comprimento e massas de 60,0k g e 100k g , respectivamente (consulte a Fig. P10.17). De
O grande músculo quadríceps na parte superior da perna termina em sua extremidade inferior em um tendão ligado à extremidade superior da tíbia (Fig. P10.77a). As forças sobre a parte inferior da perna