Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.10 - Ex. 41
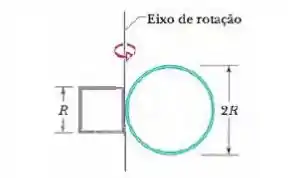
A figura abaixo mostra uma estrutura rígida formada por um aro de raio e massa e um quadrado feito de quatro barras finas de comprimento e massa . A estrutura rígida gira com velocidade constante em torno de um eixo vertical, com um período de rotação de . Supondo que e , calcule
o momento de inércia da estrutura em relação ao eixo de rotação
o momento angular da estrutura em relação ao eixo.
Passo 1
Faalaaa aii galerinha bonita, tudo tranks!? Bora lá treinar um pouco o cálculo do momento angular?
Belezoca, como queremos o momento angular total sobre um eixo, mas temos dois objetos completamente diferentes, podemos somar os momentos inércia de cada um deles, de forma que o momento de inércia total é dado como:
Show de bola, então primeiro vamos começar calculando o momento de inércia do aro . Sabemos que o momento de inércia de um aro circular em relação a um eixo que passa pelo seu centro é
Mas como o eixo está deslocado do centro, vamos usar o teorema dos eixos paralelos para encontrar o momento de inércia em relação a esse novo eixo.
Esse teorema nos diz que o momento de inércia em relação a um eixo paralelo ao que passa pelo centro de massa, vai ser:
Como a distância entre o centro de massa do aro (seu centro) e o eixo de rotação é , podemos calcular:
Passo 2
Iradoso, agora o momento de inércia do quadrado:
Aqui teremos que tomar cuidado, pois não trataremos o quadrado como sendo um objeto único, na verdade vamos calcular o momento de inércia de cada lado do quadrado, pois cada um deles vai possuir um momento de inércia diferente em relação ao eixo, sendo assim, o momento total do quadrado será a soma de todos esses momentos individuais.
O lado que está sobre o eixo de rotação não contribui para o momento de inércia. Os lados perpendiculares ao eixo de rotação tem momento de inércia:
E para o lado mais distante, vamos usar novamente o teorema dos eixos paralelos:
Como eixo que passa pelo centro de massa seria ao longo do lado do quadrado, ele também não conta para o momento de inércia, e sua contribuição seria:
Agora o momento do quadrado total vai ser a soma de todos esses momentos de inércia, tal que:
Assim o momento de inércia total vai ser:
Com e , obtemos que:
Passo 3
Belejóia, agora vamos determinar a velocidade angular, para daí poder calcular o momento angular.
Sabendo que o período de revolução é a velocidade será:
Passo 4
Agora sim podemos calcular o momento angular . Lembrando que ele se relaciona com o momento de inércia e com a velocidade angular, desse jeito aqui:
Show de bolinhaaas!
