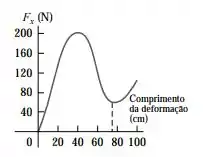
A Figura abaixo mostra como a força exercida pelo fio de um arco varia em função da distância em que a flecha é puxada para trás (o comprimento de deformação). Suponha que a mesma força seja fornecida para a flecha que se move para frente quando o fio é liberado. A deformação máxima para esse arco corresponde a um comprimento de deformação igual a 75,0 cm. Se o arco atira uma flecha de 0,0250 kg quando ele está submetido a uma deformação máxima, qual é a velocidade da flecha quando ela abandona o arco?

Pensando no trabalho como através da aproximação da curva F vesus x como uma parábola que vai de x = 0 até x = xo , teremos que quando Fo for máximo:

x

Como admitimos que a curva é uma parábola ficou fácil encontrar Fo máximo pelas formulas que já conhecemos para valores máximos e mínimos de uma parábola, não é mesmo?

Então vamos em frente. O trabalho pode ser:

Substituindo o Fx na integral e definindo os extremos como aqueles já citamos acima, vai ficar:

Tendo descoberto o valor do trabalho, usaremos a seguinte fórmula para acharmos a velocidade:

Agora que sabemos tudo o que temos que fazer, vamos aplicar os valores e resolver a questão!