Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.Problemas Adicionais - Ex. 79
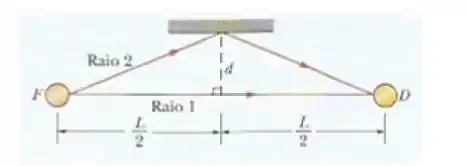
Na figura abaixo um som com um comprimento de onda de é emitido isotropicamente por uma fonte pontual . O raio de som se propaga diretamente do detector , situado a uma distância . O raio de som chega a após ser refletido por uma superfície plana. A reflexão ocorre na mediatriz do segmento da reta , a uma distância do raio . Suponha que a reflexão desloca a fase de onda sonora de . Qual é o menor valor de (diferente de zero) para o qual o som direto e o som refletido chegam a em oposição de fase e em fase.
Passo 1
Para o som chegar em em oposição de fase, as ondas dos raios e tem de interferir destrutivamente.
A condição para termos interferência destrutiva é:
Mas temos que prestar atenção a um detalhe: a reflexão desloca a a fase sonora de , assim, temos de somar esse deslocamento no lado direito da equação:
Guardem essa condição de ressonância na cachola! Vamos precisar daqui a passos!
Passo 2
Agora precisamos determinar a variação entre os deslocamentos dos raios sonoros.
Pelo desenho, é bem tranquilo de ver que o percurso feito pelo raio vai ser:
O percurso percorrido pelo raio é um pouco mais chato de ver, mas vou descomplicar pra vocês:
Vou dar um zoom na parte do desenho que importa:
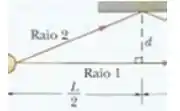
Dá pra ver que os segmentos de reta de tamanho formam um triângulo retângulo. Podemos assim aplicar o teorema de Pitágoras e determinar o percurso percorrido pelo raio , vou chamar de .
O caminho total vai ser duas vezes a hipotenusa desse triângulo.
Assim a diferença de fase fica:
Passo 3
Lembram daquela condição de ressonância que falei, então, vamos usar ela aqui! Tendo em função da distância e já que queremos o menor valor de , façamos naquela condição e igualamos as expressões!
Agora é só fazer um pouco de álgebra! Bora lá!
Agora é só substituir os valores e tirar a raiz de !
Antes de passar para a letra , vamos voltar para aquela condição de interferência DESTRUTIVA que encontramos.
Vejamos:
Mas olhando com mais atenção, não parece a condição para interferência CONSTRUTIVA???
É sim! Mas daí você se pergunta: mas como?!
Eu explico: quando o enunciado diz que a reflexão leva a um deslocamento de fase de meio comprimento de onda, ele na verdade adiciona isso à condição tanto de interferência construtiva, quanto da de destrutiva. E como cada uma delas difere apenas em meio comprimento de onda, uma acaba tendo a cara da outra nesse caso.
Para resolver a letra , vamos proceder do mesmo modo e acabar achando a condição de interferência destrutiva para esse caso (que seria construtivo se não tivesse o deslocamento adicional)
Passo 4
A condição para termos interferência destrutiva é:
Mas temos aquele deslocamento adicional, então:
O valor de continua sendo o mesmo, então podemos reciclar do passo . Como queremos a menor distância , faremos . Assim: