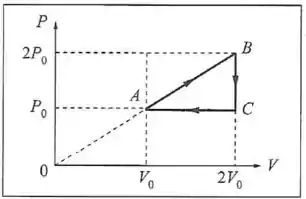
Um gás ideal de coeficiente adiabático é submetido ao ciclo da figura, onde é um segmento de reta. (a) Calcule o rendimento. (b) Mostre que ele é menor do que o rendimento de um ciclo de Carnot operando entre as mesmas temperaturas extremas.
Passo 1
Vamos começar calculando o trabalho realizado no trecho . Para isso vamos calcular a área abaixo da curva, usando a fórmula para a área do trapézio:
No processo , que é isovolumétrico, o trabalho é nulo:
E o processo é um processo isobárico, então a fórmula para o trabalho é:
Então o trabalho total ao longo do ciclo é:
Passo 2
Agora queremos calcular o calor fornecido para o gás. O gás só absorve calor no trecho , em que sua temperatura está aumentando.
Vamos começar calculando qual é a relação entre as temperaturas nesses dois pontos:
E para calcular a variação de energia interna, precisamos determinar , usando o fator que foi dado no enunciado:
Agora podemos usar a fórmula para a variação de energia interna:
E pela lei dos gases ideais, podemos escrever que :
Agora, pela primeira lei da termodinâmica:
Passo 3
Agora podemos calcular a eficiência nesse ciclo:
Vamos reescrever o termo em parênteses:
Então:
Passo 4
(b) Agora vamos calcular qual seria o rendimento de um ciclo de Carnot operando entre dois reservatórios com as mesmas temperaturas extremas:
No nosso caso, as temperaturas extremas estão em e :
Mas isso ainda não prova que o rendimento de Carnot é maior do que o calculado lá em cima.
Vamos ver em qual condição isso seria descumprido:
Ou seja, teria que ser negativo, o que não é possível. Então o rendimento de Carnot é sempre maior do que o rendimento que nós calculamos.
Resposta
(a) .
(b) .