Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.10 - Ex. 38

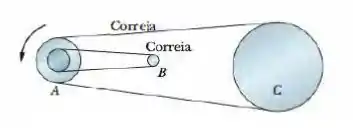
A figura abaixo mostra três discos homogêneos acoplados por correias. Uma correia passa pelas bordas dos discos A   e   C ; a outra passa por um cubo do disco A e pela borda do disco B . As correias se movem suavemente, sem deslizar nas bordas e no cubo. O disco A   tem raio R e seu cubo tem raio 0,5 R ; o disco B tem raio 0,25 R ; o disco C tem raio 2 R . Os discos B   e   C têm a mesma massa específica e mesma espessura. Qual é a razão entre o módulo do momento angular do disco C e o módulo angular do disco B ?

Passo 1

Olá pessoal, tudo bem? Vamos praticar um pouco o cálculo do momento angular?

Primeiro vamos começar calculando as massas e as velocidades angulares em função das quantidades fornecidas. Sabenso que a correia tem a mesma velocidade linear em todos seus pontos, olhando pra correia que liga os discos A e C :

v A = v C

r A ω A = r C ω C

Daqui tiramos:

ω C = ω A r A r C = ω A R 2 R

ω C = ω A 2

Agora vamos ver sobre o momento de inércia. Pra isso precisamos calcular a massa de C . A massa de C , de massa específica μ , pode ser dada pela área vezes a massa específica:

m C = π r C 2 μ

E seu momento de inércia vai ser:

I C = m C   r C 2 2 = π r C 4 μ 2 = π μ 2 R 4 2 = 8 π μ R 4

Assim o momento angular de C é:

L C = I c ω c = 8 π μ R 4 . ω A 2 = 4 π μ ω A R 4

Vamos ao momento angular de B ?

Bora!

Passo 2

Sabendo que a velocidade linear da correia que liga B e o cubo de A é o mesmo, temos:

v a = v B

ω a r a ' = ω B r B

Daqui tiramos:

ω B = ω a r a ' r B = ω A 0,5 R 0,25 R

ω B = 2 ω A

Agora vamos ver sobre o momento de inércia. Pra isso precisamos calcular a massa de B . A massa de B , de massa específica μ , pode ser dada pela área vezes a massa específica:

m B = π r B 2 μ

E seu momento de inércia vai ser:

I B = m B   r B 2 2 = π r B 4 μ 2 = π μ 0,25 R 4 2 = 1 2 9 π μ R 4

Assim o momento angular de C é:

L B = I B ω B = 1 2 9 π μ R 4 . 2 ω A = 1 2 8 π μ ω A R 4

Passo 3

  Agora podemos fazer a razão entre L C / L B :

L C L B = 4 π μ ω A R 4 1 2 8 π μ ω A R 4

Sabemos que o disco A gira rigidamente com seu cubo, então a velocidade dos dois é a mesma e podemos cortar ali em cima. Simplificando os termos semelhantes temos:

L C L B = 4 1 2 8 = 2 10 = 1024

Resposta

L C L B = 1024

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um automóvel de massa M percorre, em sentido anti-horário, uma pista circular horizontal de raio R , com velocidade escalar v constante. Conforme será visto no cap. 12, o momento angular de uma das ro
Considere um sistema isolado de duas partículas de massas m 1 e m 2 . Exprima o vetor momento angular total do sistema relativo ao seu CM em função da massa reduzida μ , do vetor posição r de m 2 em r
Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância d = 0.5 m do eixo; o ângulo θ é igual a 30 ° . O fio pas
Seja C uma curva plana fechada orientada. A área orientada S associada a C é definida como um vetor perpendicular ao plano de C, de magnitude igual à área S contida dentro de C e sentido tal que, vist
Vamos calcular a posição y da carga caindo anexada ao guincho no Exemplo 9-8 como uma função do tempo por integração numérica. Deixe a direção + y ser reta para baixo. Então, v y = d y / d t , ou t =