Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 11.Problemas - Ex. 3

Considere um sistema isolado de duas partículas de massas m 1 e m 2 . Exprima o vetor momento angular total do sistema relativo ao seu CM em função da massa reduzida μ , do vetor posição r de m 2 em relação a m 1   e da velocidade relativa v de m 2 em relação a m 1 .

Passo 1

Bora lá, galera! A gente sabe que o momento angular de uma partícula tem essa cara aqui:

L → = m r → × v →

Então temos que encontrar essas paradas aí. A situação tem essa cara aqui:

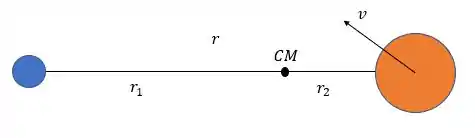
A posição do centro de massa é dada por

r → C M = m 1 r → 1 + m 2 r → 2 m 1 + m 2

O vetor posição de m 2 em relação a m 1 é

r → = r → 2 - r → 1

E a velocidade relativa de m 2 em relação a m 1 é

v → = v → 2 - v → 1

Esses são os nossos ingredientes!

Passo 2

O vetor da posição de m 1 em relação ao centro de massa é dado por

r → 1 ' = r → 1 - r → C M = r → 1 - m 1 r → 1 + m 2 r → 2 m 1 + m 2 = m 1 r → 1 + m 2 r → 1 - m 1 r → 1 - m 2 r → 2 m 1 + m 2

r → 1 ' = m 2 m 1 + m 2 r → 1 - r → 2

Reconheceu esse carinha do lado direito? É o vetor r → que calculamos no passo 1 multiplicado por - 1 !

r → 1 ' = - m 2 m 1 + m 2 r →

Derivando os dois lados da equação, relacionamos a velocidade da massa m 1 em relação ao centro de massa v → 1 ' e a velocidade da massa m 1 em relação à massa m 2

v → 1 ' = - m 2 m 1 + m 2 v →

Passo 3

Então podemos calcular o momento angular da massa m 1 em relação ao centro de massa

L → 1 ' = m 1 r → 1 ' × v → 1 ' = m 1 - m 2 m 1 + m 2 r → × - m 2 m 1 + m 2 v →

L → 1 ' = m 1 m 2 2 m 1 + m 2 2 r → × v →

Passo 4

Agora vamos calcular para a massa m 2 . O cálculo é bem parecido com o da massa m 1 :

r → 2 ' = r → 2 - r → C M = r → 2 - m 1 r → 1 + m 2 r → 2 m 1 + m 2 = m 1 r → 2 + m 2 r → 2 - m 1 r → 1 - m 2 r → 2 m 1 + m 2

r → 2 ' = m 1 m 1 + m 2 r → 2 - r → 1 = m 1 m 1 + m 2 r →

E agora é só derivar

v → 2 ' = m 1 m 1 + m 2 v →

Passo 5

Agora é só calcular o momento angular em relação ao centro de massa

L → 2 ' = m 2 r → 2 ' × v → 2 ' = m 2 m 1 m 1 + m 2 r → × m 1 m 1 + m 2 v →

L → 2 ' = m 2 m 1 2 m 1 + m 2 2 r → × v →

Show!

Passo 6

Agora basta somar os dois momentos angulares para calcular o momento angular total

L → ' = L → 1 ' + L → 2 ' = m 1 m 2 2 m 1 + m 2 2 r → × v → + m 1 2 m 2 m 1 + m 2 2 r → × v →

L → ' = m 1 m 2 2 + m 1 2 m 2 m 1 + m 2 2 r → × v →

L → ' = m 1 m 2 m 1 + m 2 m 1 + m 2 2 r → × v → = m 1 m 2 m 1 + m 2 r → × v →

Agora falta relacionar com a massa reduzida, né? Ela é dada por

1 μ = 1 m 1 + 1 m 2

Aí podemos trabalhar nessa expressão

1 μ = m 2 + m 1 m 1 m 2 → μ = m 1 m 2 m 1 + m 2

Que é exatamente o que aparece lá no momento angular total!!! :D

L → ' = μ r → × v →

Feshow! \o/

Resposta

L → ' = μ r → × v →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pedra de 2,0 kg possui uma velocidade horizontal com módulo de 12,0 m/s quando está no ponto P na Figura 10.47. a) Nesse instante, qual é o módulo, a direção e o sentido do seu momento angular em
Uma partícula viaja por um caminho circular, e o ponto P está no centro desse círculo. (a) Se o momento linear da partícula p → é dobrado, sem mudar o raio do círculo, como a magnitude do momento angu
Uma partícula pontual de massa m está se movendo com rapidez constante v ao longo de uma linha reta que passa pelo ponto P . O que você pode afirmar sobre o momento angular da partícula em relação ao
O momento angular da hélice de um pequeno avião monomotor aponta para frente. A hélice gira no sentido horário, se vista de trás. (a) Logo após a decolagem, conforme o nariz do avião inclina-se para c
Um planeta se move em uma órbita elíptica em torno do Sol, com o Sol em um dos focos da elipse, como na figura. (a) Qual é o torque em relação ao centro do sol devido à força de atração do sol sobre o