Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 62

A figura abaixo mostra um tubo estático de Pitot, um dispositivo usado para medir a velocidade de um gás. O tubo interno fica de frente para o fluido recebido, enquanto o anel de orifícios no tubo externo é paralelo ao fluxo de gás. Mostre que a velocidade do gás é dada por v = 2 g h ρ L - ρ g ρ g , onde ρ L é a densidade do líquido usado no manômetro e ρ g é a densidade do gás.

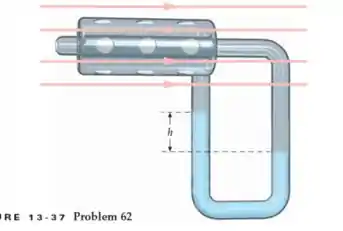
Passo 1

Okay gente, provavelmente você nunca viu um problema como esse... mas relaxa que é normal! Ele é bem estranho de começo, mas a gente digerindo ele com calma, tudo sai certinho!! Nós queremos achar a velocidade do gás, mas observando a dinâmica do problema, percebemos que essa velocidade nada mais é que uma diferença de pressões... E AÍ, O QUE LEMBRA DIFERENÇA DE PRESSÕES? Isso mesmo!! Nosso amigo Bernoulli!

Seja a primeira pressão denotar a abertura no final do tubo interno e a segunda pressão em um dos orifícios no tubo externo. Podemos aplicar o princípio de Bernoulli nesses locais e resolver a diferença de pressão entre eles. Ao equacionar essa diferença de pressão com a diferença de pressão devido à altura h da coluna de líquido, podemos expressar a velocidade do gás em função de ρ L ,   ρ g ,   g   e   h .

Passo 2

Aplicando Bernoulli para os nossos locais, temos que:

P 1 + 1 2 ρ g v 1 2 = P 2 + 1 2 ρ g v 2 2

Mas ignoramos a diferença entre as alturas das duas aberturas! Agora vamos expressar a diferença de pressão como ∆ P !

∆ P = P 1 - P 2 = 1 2 - ρ g v 2 2 - 1 2 ρ g v 1 2

Qual a velocidade do gas na entrada 1? 0 ué, porque o gás é interrompido lá em cima, então a velocidade dele é 0. Logo, v 1 = 0 . E a velocidade dele na entrada 2? É justamente a velocidade v que a gente tanto quer, porque lá o gás flui livremente. Logo, v 2 = v .

∆ P = 1 2 - ρ g v 2 2

Passo 3

Sendo A a área da seção transversal do tubo, vamos expressar a pressão na altura h na coluna de líquido cuja densidade é ρ 1 :

P 1 = P 2 + w f l u i d o   d e s l o c a d o A - B A

Onde o nosso B é a tão conhecida força de flutuação! Ela corresponde a B = ρ g A g h agindo na coluna de altura h . Portanto, substituímos:

P 1 = P 2 + ρ L g h A A - ρ g A g h A = P 2 + ρ L - ρ g g h

Ou

∆ P = ρ L - ρ g g h

Passo 4

Mas o que é o nosso ∆ P ? A gente definiu lá em cima!!

∆ P = 1 2 - ρ g v 2 2

Então basta substituirmos:

∆ P = ρ L - ρ g g h

1 2 - ρ g v   2 = ( ρ L - ρ g ) g h

Isolando o nosso v , temos que:

v = 2 g h ρ L - ρ g ρ g

Dica interessante: Esse sistema é usado para medir a velocidade do ar em aviões!

Resposta

v = 2 g h ρ L - ρ g ρ g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um grande tanque de diâmetro D está aberto para a atmosfera e contém água até uma altura H. Um pequeno orifício com diâmetro d(d
9. Dois tubinhos de mesmo diâmetro, um retilíneo e o outro, com um cotovelo, estão imersos numa correnteza horizontal de água de velocidade v . A diferença entre os níveis da água nos dois tubinhos é
Uma ampulheta é formada, de cada lado, por um tronco de cone circular de altura h = 10c m , raio da base maior R = 10c m , e raio da base menor r = 0,1c m . Após enchê-la de água até a metade, ela é i
A figura ilustra uma variante do tubo de Pitot, empregada para medir a velocidade v de escoamento de um fluido de densidade ρ . Calcule v em função do desnível h entre dois ramos do manômetro e da den
Um medidor tipo Venturi é inserido numa tabulação inclinada de raio R , onde se escoa um fluido de densidade ρ . O estreitamento tem raio r e os ramos do manômetro são inseridos em pontos de alturas z