Uma ampulheta é formada, de cada lado, por um tronco de cone circular de altura , raio da base maior , e raio da base menor . Após enchê-la de água até a metade, ela é invertida. (a) Calcule a velocidade inicial de descida do nível da água; (b) Calcule a velocidade de descida do nível depois de ele ter baixado de ; (c) Que forma deveria ter a superfície lateral (de revolução) da ampulheta para que o nível da água baixasse uniformemente (relógia de água)?
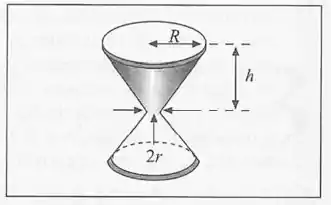
Passo 1
(a) Para calcular a velocidade inicial de descida, vamos começar aplicando a equação de Bernoulli entre dois pontos e :
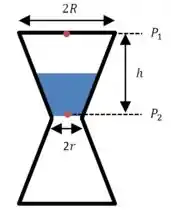
Ambos os pontos estão na superfície do volume de líquido, então :
Podemos definir que a altura do ponto é e para o ponto teremos :
Por enquanto temos duas variáveis e só uma equação.
Passo 2
Podemos encontrar nossa segunda equação da seguinte forma:
Então temos um sistema:
E a velocidade de descida do nível da água (que o enunciado pediu) é a velocidade de descida do ponto , então vamos resolver o sistema para encontrar :
E substituindo os valores numéricos:
Passo 3
(b) A fórmula que nós acabamos de descobrir continua válida durante toda a descida. A única diferença é o raio da parte superior.
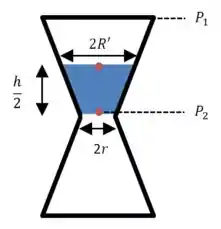
E então:
E podemos calcular usando semelhança de triângulos:
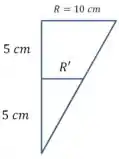
Então:
Passo 4
(c) Vamos tentar determinar a forma da superfície lateral para que o nível de água abaixe uniformemente.
Vamos criar um sistema de coordenadas em que é a altura a partir do centro da ampulheta e é a distância de cada ponto da superfície até o eixo:
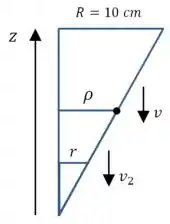
Dessa vez a equação da continuidade dá:
E a equação de Bernoulli (conforme a segunda equação do nosso sistema lá de cima) fica:
Como a fração dentro dos parênteses deve ser bem maior do que , podemos aproximar por:
Resposta
(a) A velocidade inicial de descida do nível da água deve ser de .
(b) A velocidade de descida do nível depois de ter baixado é .
(c) , onde é a altura a partir do centro, é a velocidade de descida do nível e é a distância até o eixo.