Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 2.Problemas - Ex. 10

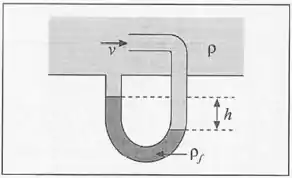
A figura ilustra uma variante do tubo de Pitot, empregada para medir a velocidade v de escoamento de um fluido de densidade ρ . Calcule v em função do desnível h entre dois ramos do manômetro e da densidade ρ f do fluido manométrico.

Passo 1

Vamos começar escolhendo dois pontos para aplicarmos a condição de equilíbrio hidrostático:

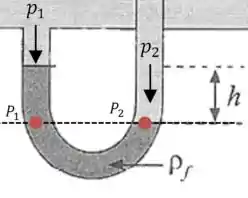
A pressão nos dois pontos vermelhos deve ser igual, então:

p 1 + ρ f g h = p 2 + ρ g h

p 2 - p 1 = ρ f - ρ g h

Passo 2

Agora vamos aplicar a equação de Bernoulli sobre dois pontos que estão sujeitos às mesmas pressões p 1 e p 2 , mas em pontos mais convenientes para nós.

Vamos “erguer” os pontos até a altura do cano:

As pressões nos dois pontos ainda são p 1 e p 2 , mas agora o ponto P 2 está em um ponto de estagnação ( v 2 = 0 ) e P 1 está em um ponto onde v 1 = v .

Vamos montar a equação de Bernoulli:

p 1 + ρ g z 1 + 1 2 ρ v 1 2 = p 2 + ρ g z 2 + 1 2 ρ v 2 2

Como z 1 = z 2 :

p 1 + 1 2 ρ v 1 2 = p 2 + 1 2 ρ v 2 2

p 2 - p 1 = 1 2 ρ v 1 2 - v 2 2

Fazendo v 2 = 0 e v 1 = v :

p 2 - p 1 = 1 2 ρ v 2

E substituindo com a fórmula que encontramos no passo anterior:

ρ f - ρ g h = 1 2 ρ v 2

v = 2 g h ρ f ρ - 1

Resposta

A velocidade é v = 2 g h ρ f ρ - 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um balde cilíndrico, aberto na parte superior, possui diâmetro de 10,0 cm e altura igual a 25,0 cm. Um orifício circular com área da seção reta igual a 1,50 c m 2 é feito no centro da base do balde. A
Dois grande tanques abertos A e F (Figura 14.44) contém o mesmo liquido. Um tubo horizontal BCD, que tem uma constrição C e é aberto ao ar no ponto D, sai da base do tanque A, e um tubo vertical E par
Um grande tanque de diâmetro D está aberto para a atmosfera e contém água até uma altura H. Um pequeno orifício com diâmetro d(d
9. Dois tubinhos de mesmo diâmetro, um retilíneo e o outro, com um cotovelo, estão imersos numa correnteza horizontal de água de velocidade v . A diferença entre os níveis da água nos dois tubinhos é
Uma ampulheta é formada, de cada lado, por um tronco de cone circular de altura h = 10c m , raio da base maior R = 10c m , e raio da base menor r = 0,1c m . Após enchê-la de água até a metade, ela é i