Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.7 - Ex. 67
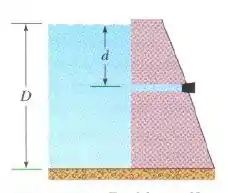
Na figura, a água doce atrás de uma represa tem uma profundidade . Um cano horizontal de de diâmetro atravessa a represa a uma profundidade . Uma tampa fecha a abertura do cano. (a) Determine o módulo da força de atrito entre a tampa e a parede do tubo. (b) A tampa é retirada. Qual é o volume de água que sai do cano em ?
Passo 1
Show de bolinhas pessoal, nesse exercício aqui, na letra (a) queremos encontrar o módulo da força de atrito entre a tampa e a parede do tubo, que é basicamente a força que segura a tampa onde ela está.
Como o sistema está em equilíbrio, a força que segura a tampa é a mesma que a força com que a água empurra a tampa! Ou seja, é só a gente calcular a força que a água da represa exerce ali.
Então vamos lá, onde aparece a força nas nossas fórmulas de fluidos? Ah sim, na definição da pressão:
Então já temos aí a equação que precisamos completar para achar o módulo da força.
Passo 2
Vamos começar calculando o valor de , usando o diâmetro do cano, que o enunciado dá:
Logo:
Agora fica faltando só a pressão naquela profundidade. Essa também é uma fórmula que conhecemos bem:
Onde é a profundidade e é a densidade da água ().
E a força vai ser:
E essa vai ser a resposta da letra (a).
Obs.: Não incluímos a pressão atmosférica nessa conta, porque ao mesmo tempo em que ela ajuda a água a empurrar a tampa, ela também ajuda a tampa a empurrar a água. Se a tampa estivesse totalmente submersa (sem contato com a atmosfera), teríamos que incluir a pressão atmosférica na conta da pressão!
Passo 3
A letra (b) pede o volume de água que sai quando retiramos a tampa em um intervalo de . Vamos primeiro converter esse intervalo para segundos:
E o volume de água que sai nesse intervalo vai ser simplesmente o produto entre a vazão:
E esse intervalo de tempo. Então:
Onde é a velocidade da água no cano, e é a área da seção reta do cano. Nesse caso, já calculamos e , mas falta descobrir a velocidade.
Sabemos que nesses casos a velocidade que escoa por um cano submerso em uma profundidade em um recipiente é:
Substituindo na equação acima:
Resposta
(a)
(b)