Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.7 - Ex. 56
Dois tanques e , ambos com uma grande abertura no alto, contêm líquidos diferentes. Um pequeno furo é feito no lado de cada tanque à mesma distância abaixo da superfície do líquido, mas o furo do tanque tem metade da seção reta do furo do tanque . (a)Qual é a razão entre as massas específicas dos llíquidos se a vazão mássica é a mesma para os dois furos? (b)Qual é a razão entre as vazões volumétricas dos dois tanques? (c) Em um certo instante, o líquido do tanque está acima do furo. A que altura acima do furo o líquido do tanque deve estar nesse instante para que os tanques tenham vazões volumétricas iguais?
Passo 1
Fala galerinha bonita, show de bolinhas com vocês?
(a)Nessa questão temos um exemplo de fluido que não está em uma situação de repouso. Nesse caso, devemos usar como ferramenta a Equação de Bernoulli. Segundo ela, em todo escoamento de fluido incompressível a expressão abaixo representa uma constante
, tal que , , e representam a pressão no ponto considerado, a densidade do fluido, sua velocidade e a altura do ponto com relação a um referencial arbitrário.
Passo 2
Agora, vamos analisar o problema com base na equação de Bernoulli, considerando o referencial de altura como localizado nas superfícies dos líquidos de ambos os recipientes, assim como o indicado na figura.
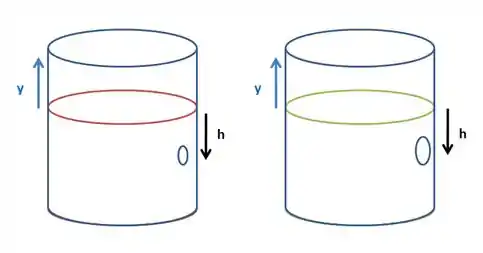
Vamos aplicar a equação de Bernoulli para analisar o escoamento do fluido contido no recipiente à esquerda. Vamos aplicar a expressão em dois pontos desse fluido: na superfície do líquido e em um ponto localizado no furo. Assim, temos:
Onde o índice e o índice se referem a superfície e ao furo respectivamente.
Passo 3
Vamos interpretar os elementos das expressões acima. Olhando primeiro para a superfície. Com a presença do furo, o líquido flui para baixo na superfície com uma velocidade . Vamos relacionar essa velocidade com a velocidade do escoamento no furo por meio da equação da continuidade:
Agora é hora de atentar para duas informações dadas no enunciado: os recipientes possuem uma grande abertura no alto e os furos têm áreas pequenas. Podemos considerar que essa informação indica que:
Isolando na equação da continuidade o valor de , temos:
Como a área do furo é muito menor que a da superfície, a razão é muito pequena. Consequentemente, podemos considerar que, com relação à velocidade do fluido no furo, é bem pequena, podendo ser desprezada na equação de Bernoulli. Lembre-se, então que, sempre que a área do furo for muito pequena com relação à da superfície, deve ser desprezada.
Passo 4
Aplicando então a equação de Bernoulli, uma vez que , e , temos:
Como o furo é aberto para a atmosfera, . Então, a expressão anterior fica assim: , ou seja:
Passo 5
Considerando a expressão anterior e usando o fato de que as vazões dos furos e são as mesmas, temos:
Como o furo em possui o dobro da área em segundo o enunciado , temos que
Passo 6
(b) Lembrando que a vazão é representada pelo produto entre a área e a velocidade do fluido, temos:
, pois , como encontramos no passo 4.
Passo 7
(c) Nesse caso, ocorre que as alturas dos furos com relação às superfícies dos líquidos são diferentes. Vamos considerá-las como iguais a e . Se as vazões volumétricas são iguais, ocorre que
Logo, .
Passo 8
Da equação de Bernoulli analisada inicialmente, decorre que:
Logo, temos que
Então, temos como resultado: