Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 14
Na figura, um andaime horizontal, de de comprimento e massa homogênea de está suspenso de um edifício por dois cabos. O andaime tem várias latas de tinta empilhadas. A massa total das latas de tinta é . A tensão do cabo à direita é . A que distância desse cabo está o centro de massa do sistema de latas de tinta?
Passo 1
Fala galerinha do RespondeAí, tudo belezinha?
Nesse exercício aqui, temos que o andaime está em equilíbrio no ar sob a ação de duas forças lateriais, devido aos cabos de sustentação, e também as forças pesos do próprio andaime e das latas de tintas.
A malandragem desse exercício, é que não sabemos onde está o centro de gravidade das latas de tintas, onde a força peso delas atuam, além disso as tensões nos cabos laterais NÃO SÃO IGUAIS, ou seja, a tensão no cabo da direita é , mas não quer dizer que a tensão no cabo da esquerda também seja!!
Sabendo disso, o enunciado pede pra gente calcular justamente a distância (em relação ao cabo da direita) que o centro de massa das latas se encontra.
Pra isso, podemos primeiro desenhar o diagrama de corpo livre para o andaime, tal que:
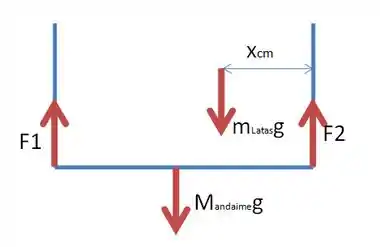
Onde e são as tensões nos cabos da esquerda e da direita respectivamente, enquanto que é a força peso das latas e a força peso do andaime, com e sendo as massas das latas e do andaime. Queremos descobrir o valor de , então bora lá!
Passo 2
Show de bolinhas, pra gente resolver essa brincadeira, podemos lembrar que no equilíbrio, a soma dos torques no sistema deve ser nulo:
O detalhe importante é que não sabemos o valor de , MAAAASSSSS, como a gente é malandro, podemos calcular o somatório dos torques em relação ao ponto que está atuando, vamos chamar de ponto :
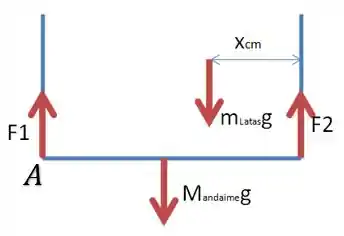
Isso é bom, porque agora a força não gera torque em relação ao ponto , e não precisamos saber seu valor para calcular o torque em relação a , logo a distância da forças das latas até o ponto será , de modo que:
Isolando , obtemos que:
Substituindo os valores que o enunciado nos deu, , :
Portanto: