Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.Problemas Adicionais - Ex. 59
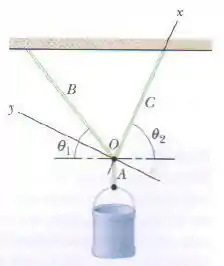
Na figura, uma caçamba de está suspensa por um cabo que, por sua vez, está preso no ponto a dois outros cabos, e , que fazem ângulo e com a horizontal. Determine a tensão (a) do cabo , (b) do cabo e (c) do cabo . (Sugestão: para não ter que resolver um sistema de duas equações com duas incógnitas, defina os eixos da forma mostrada na figura.)
Passo 1
Olhando a imagem dá pra ver que o cabo é puxado para baixo pelo peso da caçamba. Isso quer dizer que a tensão sobre ele tem que ser exatamente igual a esse peso, do contrário o sistema não estaria em equilíbrio.
Ou seja, pela condição de equilíbrio:
Passo 2
Agora vamos decompor os vetores que representam as tensões sobre os cabos e :
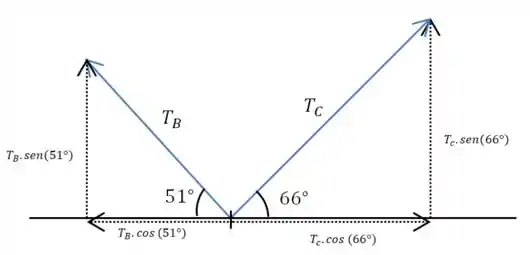
Vamos escrever as seguintes igualdades:
E assim chegamos a um sistema.
Passo 3
Resolvendo os senos em uma calculadora:
Podemos resolver esse sistema sem problemas.
Isolando na segunda equação:
E substituindo na primeira:
E agora substituindo isso de novo:
Resposta
(a)
(b)
(c)