Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 61

Uma placa de massa M, com a forma de um triângulo equilátero, está suspensa por um de seus vértices, e uma massa m está suspensa no outro vértice. Se a base do triângulo forma um ângulo de 6,0° cm a horizontal, qual é a razão ?

Passo 1

Beleza galera, primeiro vamos desenhar o triângulo equilátero de massa M (representado em preto), quando penduramos uma massa m o triangulo rotacional, e gira um ângulo (representado de vermelho):

O triângulo equilátero possui os três ângulos iguais a 60° e os três lados iguais, 2a. O centro de massa ou baricentro do triângulo divide as medianas em uma proporção de 2:1. Como todos os lados são iguais, as medianas também serão, então precisamos calcular somente uma.

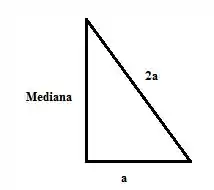
Lembrando que:

Como o centro equivale a ⅓ da distância da mediana a partir do ponto médio, e ⅔ da distância da mediana a partir do vértice:

Racionalizando

Até aqui bem tranquilo, né? O que não podemos esquecer é que, quando o triângulo rotacional um ângulo , o centro de massa rotaciona para . Assim como o centro de massa, o vértice cujo m está pendurado rotaciona para

Agora que temos estes dados podemos desenhar novamente o problema:

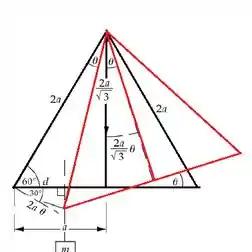
Passo 2

Muito bem, quando o corpo de massa m é pendurado em um dos vértices do triângulo, este rotaciona e atinge o equilíbrio o equilíbrio, ou seja:

Vamos usar aqui a segunda condição, já que houve uma rotação do corpo. O torque é calculado como:

Onde r é a distância entre a força e o eixo de rotação. A escolha do eixo será muito importante, e aqui vamos escolher a mediana do triângulo inicial (o preto!), que vai do topo até a base.

Beleza ! Quando fazemos isso percebemos que quando m é pendurado, a força peso que atua sobre ele estará a uma distância do eixo de rotação.

Para calcular usamos o novo triângulo formado depois da sua rotação:

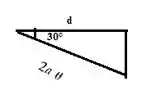
Então:

Agora nós temos tudo o que precisamos para achar o torque !!

Passo 3

Então galera, neste sistema nós teremos duas forças atuando. A primeira é a força peso sobre o corpo m, dado por:

Mas calma que não é só essa não ! o triângulo também tem uma massa M e também terá a força peso atuando sobre seu novo centro de massa, que vai estar a uma distância do eixo de rotação, como já vimo. Então neste caso:

Já temos o torque agora só precisamos saber o sentido de rotação. Por convenção se uma determinada força for capaz de girar o corpo no sentido anti-horário seu sinal será positivo. A força do corpo m é capaz de girar a barra no sentido anti-horário (+), já a força de M gira no sentido horário (-).

Sendo assim: