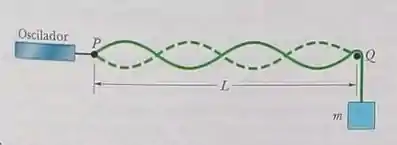
Na figura, uma corda presa a um oscilador senoidal no ponto e apoiada em um suport no ponto é tensionada por um bloco de massa . A distância entre e é e a freqüência do oscilador é . A amplitude do deslocamento do ponto é suficientemente pequena para que esse ponto seja considerado um nó. Também existe um nó no ponto . Uma onda estacionária aparece quando a massa do bloco é ou , mas não aparece para nenhuma massa entre esses dois valores. Qual é a massa específica linear da corda?

Quando uma onda estacionária aparece?

Sempre que é um número inteiro! A questão nos fala que “... uma onda estacionária aparece quando a massa do bloco é ou , mas não aparece para nenhuma massa entre esses dois valores”. Isso significa que modos de vibração e aparecem para essas duas massas.

Ou seja:

Para o bloco de :

Para o bloco de

Dividindo as duas últimas equações, a gente obtém a equação abaixo:

Agora, vamos precisar de certo “matematiquês” para encontrar , lembrando que ele deve ser um número inteiro, já que a onda formada é estacionária.

Desenvolvendo a expressão acima, a gente tem:

Podemos resolver a equação do segundo grau a partir da expressão acima, ou então ir tentando vários valores de até chegar ao resultado. Testando a gente encontra , que é um valor bem próximo ao demonstrado acima. Então, a gente pode concluir que .

Substituindo em , vem: