Na figura, um alpinista de está subindo por uma chaminé na pedra com as mãos puxando um lado da chaminé e os pés pressionando o lado oposto. A chaminé tem uma largura e o centro de massa do alpinista está a uma distância horizontal m da chaminé. O coeficiente de atrito estático entre mãos e rocha é e entre as botas e a pedra é .
a) Qual é a menor força horizontal das mãos e dos pés que mantém o alpinista estável?
b) Para a força horizontal do item (a), qual deve ser a distância vertical entre as mãos e os pés?
c) Se o alpinista encontra uma pedra molhada, para a qual os valores de e são menores, o que acontece com a resposta do item (a)?
d) E a resposta do item (b) ?
Passo 1
Fala galerinha do RespondeAí, tudo beleza?
Nesse exercício aqui temos um alpinista de se segurando em uma chaminé com de largura.
Sabendo que o alpinista está em equilíbrio, e que o coeficiente de atrito estático entre mãos e rocha é e entre as botas e a pedra é , na letra (a) o enunciado pede pra gente encontrar a menor força horizontal das mãos e dos pés que mantém o alpinista estável.
Iradoso, então se a gente desenhar as forças que atuam no sistema, teremos:
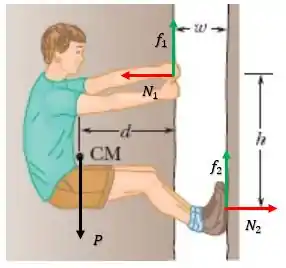
Onde e são as forças que o alpinista exerce sobre as laterais da chaminé através das mãos e dos pés respectivamente. Enquanto que e são as devidas forças de atrito resultantes de e , além disso temos a força peso do alpinista.
Do equiíbrio vertical das forças, temos:
Passo 2
Belezoca, agora do equilíbrio das forças exercidas na horizontal, a gente tem:
Então, considerando a expressão do Passo 1 fica assim:
Isolando :
Como o enunciado nos deu que e , com um alpinista pesando , obtemos que:
Passo 3
(b)Agora pra gente encontrar a altura , podemos considerar o equilíbrio de torques com relação ao ponto de contato entre os pés do alpinista e a parede, temos:
Então isolando a altura :
Logo:
Passo 4
Para responder a essa pergunta, vamos lembrar da expressão que encontramos no item a)
Se o denominador da equação acima diminui, o valor de aumenta (para um mesmo valor de ). Então, podemos perceber que se a pedra estiver molhada, a resposta do item a) aumenta.
Passo 5
(d)Vamos agora desenvolver a expressão do passo 3:
Nesse caso, como aumenta, o denominador de diminui, o que faz com que diminua. Então, se os coeficientes de atrito diminuem, também diminui.
Resposta
(a)
(b)
(c)Aumenta
(d)Diminui