Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.Problemas Adicionais - Ex. 66
A figura mostra o deslocamento do ponto de uma corda situado em em função do tempo quando uma onda passa pelo ponto. A escala do eixo é definida por . A onda tem a forma . Qual é o valor de ? (Atenção: as calculadoras nem sempre fornecem o valor correto de uma função trigonométrica inversa; por isso, verifique se o valor obtido para é o valor correto, substituindo-o na função ,
usando um valor numérico qualquer para e plotando a função assim obtida.)
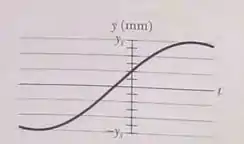
Passo 1
Como diz o enunciado, o gráfico nos mostra o deslocamento de um ponto situado em . Então, ele representa graficamente a onda . Analisando um pouquinho mais o gráfico, a gente tem:
- Em
- O maior valor de é
Usando esses dois fatos, a gente tem como resultado:
Então: ou . Eita, e agora, qual ângulo escolher?
Passo 2
Pra a gente saber qual escolha fazer, vamos precisasr derivar a equação de dada inicialmente pra verificar o sinal da velocidade encontrada. Fazendo isso, temos:
Como em a derivada da posição é positiva, deve ocorrer que e então , ou seja: . Então: ou .
Em outras palavras, como , : ou . O único ângulo dos selecionados acima que se enquadra em algum desses intervalos é .