Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.Problemas Adicionais - Ex. 57
Na figura, uma esfera de está presa por um cabo sobre um plano inclinado sem atrito que faz um ângulo com a horizontal. O ângulo é . Calcule a tensão do cabo.
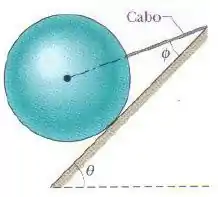
Passo 1
Vamos desenhar a situação e dar nome às forças:
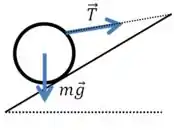
Vamos começar calculando os componentes de cada força na direção do plano inclinado.
Começando pela tração:
E para o peso é só usar a famosa fórmula do plano inclinado:
Que fica negativa porque o peso puxa a esfera plano abaixo.
O diagrama com as componentes que calculamos fica assim:
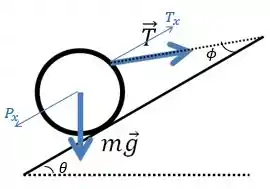
Passo 2
Beleza, como a esfera está presa e parada, vamos usar a condição de equilíbrio:
Ou seja:
Agora é só isolar a tração:
Resposta
A tensão no cabo é .
Exercícios de Livros Relacionados
A Figura mostra uma viga horizontal homogênea, de massa m b e comprimento L , que é sustentada à esquerda por uma dobradiça presa a uma parede e à direita por um cabo que faz um ângulo θ com a horizon
Depois de uma queda, um alpinista de 95k g está pendurado na extremidade de uma corda originalmente com 15m de comprimento e 9,6m m de diâmetro, que foi esticada de 2,8c m . Determine (a) a tensão, (b
Na figura, uma caçamba de 817k g está suspensa por um cabo A que, por sua vez, está preso no ponto 0 a dois outros cabos, B e C , que fazem ângulo θ 1 = 51,0 ° e θ 2 = 66,0 ° com a horizontal. Determi
Na Figura um pacote de massa m está pendurado em uma corda que, por sua vez, está presa à parede através da corda 1 e ao teto através da corda 2 . A corda 1 faz um ângulo φ = 40 ° com a horizontal; a