Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.Problemas Adicionais - Ex. 109
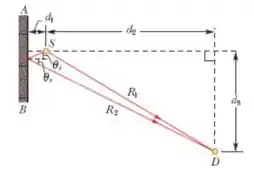
Na figura, uma fonte pontual de ondas sonoras está nas proximidades de uma parede . As ondas produzidas pela fonte chegam a um detector de duas formas: diretamente (raio ) e depois de serem refletidas pela parede, com um ângulo de incidência igual ao ângulo de reflexão (raio ). Suponha que a reflexão do som na parede causa um deslocamento de fase de . Se as distâncias são , e , determine (a) a menor frequência e (b) a segunda menor frequência para a qual os raios e estão em fase ao chegaram ao detector .
Passo 1
Vamos começar analisando a diferença de caminho entre a luz que vai de até pelo raio e a que reflete na parede e segue .
Para isso vamos aplicar o teorema de pitágoras:
E para o caminho temos que fazer um pequeno “prologamento” do raio para formar um triângulo retângulo:
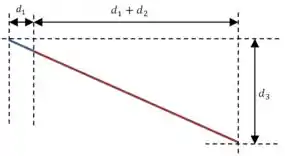
Então a diferença de caminho entre os raios é:
Passo 2
Mas além da diferença de caminho, temos um deslocamento de fase de gerado pela reflexão contra a parede.
Então a diferença total é:
Se os raios chegam em fase até o detetor , isso quer dizer que a diferença é um múltiplo do comprimento de onda :
Passo 3
Mas nosso objetivo aqui é calcular frequências, por isso precisamos substituir na equação usando a seguinte fórmula:
Então a nossa equação fica:
Onde , então:
Passo 4
(a) Então a menor frequência acontece quando , ou seja:
(b) E a segunda menor frequência acontece quando , então:
Resposta
(a) .
(b) .