Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 9.Problemas - Ex. 8
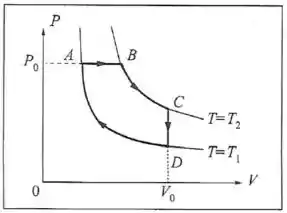
Um mol de um gás ideal descreve o ciclo representado na figura no plano , onde e são isotermas. Calcule o trabalho total associado ao ciclo, em função de , , e .
Passo 1
Vamos começar pelo caminho , que é um processo isobárico. Nesse caso o trabalho segue a seguinte fórmula:
E precisamos calcular e usando a lei dos gases ideais:
E sabendo que , e :
Substituindo na fórmula de cima:
Passo 2
Para o caminho , que é um processo isotérmico, temos que usar a seguinte fórmula:
E usando , e :
E fazemos praticamente a mesma coisa para o caminho , que também é isotérmico:
Já no caminho , que é isovolumétrico, o trabalho é nulo.
Passo 3
Então o trabalho total é:
Como , podemos simplificar um pouco a expressão:
Uma observação importante: dê uma olhada nesse último logaritmo, ele foi escrito a partir da seguinte expressão:
E como , teremos o logaritmo de um número menor do que , que portanto será um número negativo.
Como esse termo se refere ao trajeto , em que o volume está diminuindo, faz sentindo que o trabalho tenha sinal negativo.
Resposta
O trabalho total é .