de (para o qual ), à pressão de atm e temperatura de , é comprimido adiabaticamente até o volume de e depois resfriado, a volume constante, até voltar à pressão inicial. Finalmente, por expansão isobárica, volta à situação inicial. (a) Represente o processo no plano , indicando (atm), (l) e (K) para cada vértice do diagrama. (b) Calcule o trabalho total realizado; (c) Calcule e para cada etapa.
Passo 1
Vamos começar usando as informações do enunciado para fazer um gráfico:
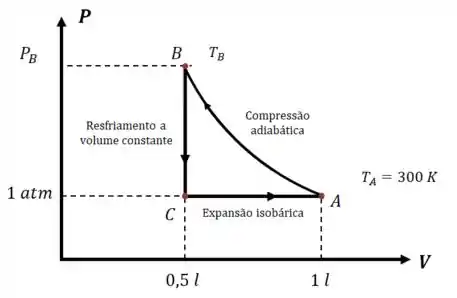
Para completar o diagrama falta encontrar , e .
Para calcular , vamos aproveitar o fato de que o processo é adiabático:
Passo 2
Para calcular a temperatura , vamos usar a lei dos gases ideais para comparar os pontos e :
E fazemos o mesmo para a temperatura , agora comparando os pontos e :
Agora é só completar o gráfico:
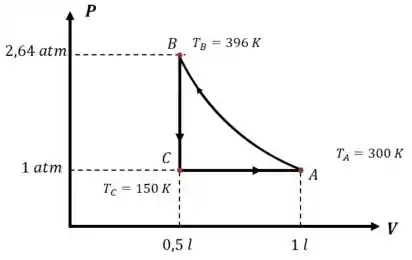
Passo 3
(b) Para calcular o trabalho total realizado, primeiro vamos considerar o processo .
Como esse processo é adiabático, a primeira lei da termodinâmica diz que:
E para calcular a variação de energia interna, podemos usar a seguinte fórmula:
Onde o número de moles do gás pode ser calculado usando a lei dos gases ideais em qualquer ponto do gráfico:
E falta também calcular . Para isso podemos usar o fato de que e a seguinte fórmula:
Substituindo na fórmula:
E então:
Passo 4
O trecho é isovolumétrico, então o trabalho é nulo. Já o trecho é isobárico, então podemos calcular o trabalho usando a seguinte fórmula:
Convertendo e :
Agora é só somar esses dois valores:
Passo 5
(c) E finalmente, queremos calcular a variação da energia interna e o calor para cada etapa.
No trajeto , que é adiabático, temos e já calculamos .
No trajeto , que é isovolumétrico, o trabalho é nulo, então :
No trajeto , a primeira lei da termodinâmica dá:
E usando a mesma fórmula de antes:
Resposta
(a) Ver desenho.
(b)
(b) e . , . e .