Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 126

A figura mostra um cilindro maciço de massa e raio , ao qual foi preso um segundo cilindro maciço, de massa e raio . Um cordão é enrolado em torno do cilindro menor. O cilindro maior está sobre uma superfície horizontal. O coeficiente de atrito estático entre o cilindro maior e a superfície é . Se uma leve tensão é aplicada ao cordão, na direção vertical, o cilindro rolará para a esquerda; se a tensão é aplicada horizontalmente para a direita, o cilindro rolará para a direita. Determine o ângulo entre o cordão e a horizontal para o qual o cilindro permanece estacionário quando uma leve tensão é aplicada ao cordão.

Passo 1

Eu representei aqui as forças que agem no cilindro quando ele está parado.

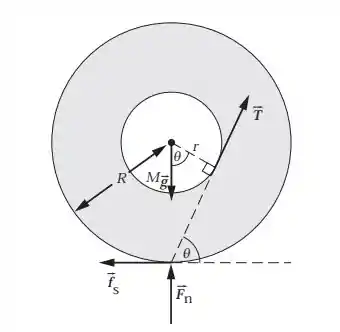
A primeira coisa que temos que perceber é que se a tensão é pequena, não pode haver escorregamento, e o sistema vai rolar. Agora considere o ponto de contato do cilindro com a superfície como o ponto pivô. Se o torque nesse ponto é quase nulo, o sistema não rola. Isso ocorre quando a linha de ação da tensão passa pelo ponto pivô.

Passo 2

Olha lá pro nosso diagrama então: o ângulo ali de baixo se transfere lá pra cima. Então naquele triângulo formado pelo centro, pelo ponto de tangência do circulo menor e pelo ponto pivô. A hipotenusa desse triângulo é e aquele cateto colado no ângulo é .

Logo,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No sistema descrito no problema 120, as constantes de força valem 60 N / m . O sistema parte do repouso e acelera lentamente até que as massas estejam a 0,80 m do centro do cilindro. Qual foi o trabal

Um bastão uniforme tem comprimento L e massa M e pode girar livremente em torno de um eixo horizontal em uma de suas extremidades, como mostrado na figura. O bastão é largado do repouso em θ = θ 0 . M

Calcule o torque, em relação à origem, da força gravitacional F → = - m g j ^ que atua sobre uma partícula de massa m localizada em r → = x i ^ + y j ^ , e mostre que este torque é independente da coo

Uma força de magnitude F é aplicada horizontalmente, no sentido - x , na borda de um disco de raio R , como mostrado na figura 10-42. Escreva F → e r → em termos de vetores unitários i ^ ,j ^ e k ^ ,