Um bastão uniforme tem comprimento L e massa M e pode girar livremente em torno de um eixo horizontal em uma de suas extremidades, como mostrado na figura. O bastão é largado do repouso em θ = θ 0 . Mostre que as componentes paralela e perpendicular da força exercida pelo eixo sobre o bastão são dadas por f = 1 2 M g 5 c o s θ - 3 c o s θ 0 e F = 1 4 M g s e n θ , onde f é a componente paralela à barra e F é a componente perpendicular à barra.

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 129

Um bastão uniforme tem comprimento e massa e pode girar livremente em torno de um eixo horizontal em uma de suas extremidades, como mostrado na figura. O bastão é largado do repouso em . Mostre que as componentes paralela e perpendicular da força exercida pelo eixo sobre o bastão são dadas por e , onde é a componente paralela à barra e é a componente perpendicular à barra.

Passo 1

Bora lá, a última do capítulo pra gente fechar rotações! A situação tá esquematizada aqui:

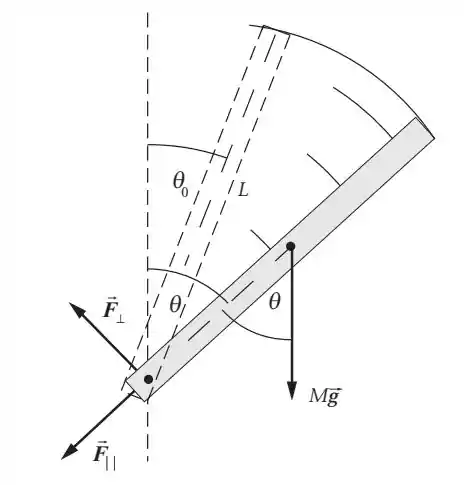
Representei o sistema em duas posições, uma com ângulo e outra com ângulo com a vertical. O desenho mostra todas as forças que atuam na barra. Essas forças vão fazer a barra girar!

Passo 2

Vamos começar conservando energia: no início ele estava na posição com , e aí rodou, adquirindo energia cinética rotacional e ficando com outra energia potencial gravitacional.

Substituindo o momento de inércia da barra:

Passo 3

Na direção da barra aparece a resultante centrípeta por causa da rotação:

Substituindo aqui o que achamos ali em cima:

Passo 4

Relacionando a aceleração tangencial do centro de massa com a sua aceleração angular:

Mas da segunda lei de Newton para a rotação:

Daí,

Essa aceleração pode, marotamente, ser escrita como a soma da componente perpendicular da gravidade mais a expressão , significando que a aceleração tangencial é a soma da aceleração da gravidade com a aceleração devido à força.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você está projetando um torno mecânico, parte de qual consiste em um cilindro uniforme de 90k g de massa e 0,40m de raio, montado de forma a girar sem atrito em torno de seu eixo. O cilindro é acionad

(a) Duas estrelas, de massas m 1 e m 2 , estão localizadas em r 1 → e r 2 → em relação a uma origem O , como mostrado na Figura 10-45. Elas exercem, uma sobre a outra, forças de atração gravitacional

Um bloco de massa m = 5,0k g desliza para baixo de uma superfície horizontal inclinada a 36,9º com a horizontal (Figura 10.55). O coeficiente de atrito cinético é 0,25. Um fio amarrado ao bloco é enro

A hélice propulsora de um avião possui comprimento de 2,08m (de uma extremidade a outra) e sua massa é de117k g . Logo no início do funcionamento do motor, ele aplica um torque de 1950N ⋅ m na hélice,

Calcule o torque (módulo, direção e sentido) em torno de um ponto O de uma força F → em cada uma das situações esquematizadas na Figura 10.37. Em cada caso, a força F → e a barra estão no plano da pág