Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 27
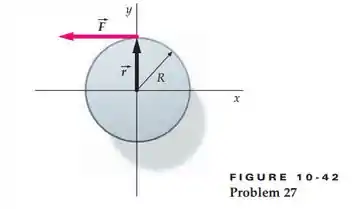
Uma força de magnitude é aplicada horizontalmente, no sentido , na borda de um disco de raio , como mostrado na figura 10-42. Escreva e em termos de vetores unitários e , e calcule o torque produzido por esta força em relação à origem no centro do disco.
Passo 1
Primeiro, vamos expressar os vetores e em termos dos unitários:
E para :
Passo 2
Lembrete:
Calculando o torque com relação ao centro do disco, temos:
Passo 3
Lembrete:
Portanto,
Resposta
Exercícios de Livros Relacionados
Até hoje se discute de que forma os pesados lintéis (blocos horizontais de pedra) foram colocados sobre blocos verticais em Stonehenge. Um possível método foi testado em uma pequena cidade tcheca. Um
(a) No exemplo 10 - 8 , quando o rotor explodiu qual foi o momento, em relação ao eixo de rotação, liberado para o ambiente? (b) Supondo que a maioria dos peadços do rotor parou de se mover no máximo
A figura abaixo mostra a energia potencial U ( x ) de uma bola maciça que pode rolar ao longo de um eixo x . A escala do eixo U é definida por U s = 100 J . A bola é homogênea, rola suavemente e possu
12.25. O momento de inércia de um objeto vale 2,0k g ⋅ m 2 . Sua velocidade angular cresce a uma taxa de 4,0 rad/s por segundo. Qual é o torque exercido sobre o objeto?
12.26. Um objeto cujo momento de inércia vale 4,0 kg m^2 experimenta o torque representado na figura EX12.26. Qual é a velocidade angular do objeto em t=3,0 s? Considere que ele parta do repouso.