A figura (a) mostra três partículas no eixo x. A partícula 1 (com uma carga de +5,0 μC) e a partícula 2 (com uma carga de +3,0 μC) são mantidas fixas no lugar, separadas por uma distância d = 4,0 cm. A partícula 3 pode ser deslocada ao longo do eixo x, à direita da partícula 2. A figura (b) mostra a energia potencial elétrica U do sistema de três partículas em função da coordenada x da partícula 3. A escala do eixo vertical é definida por = 5,0 J. Qual é a carga da partícula 3?
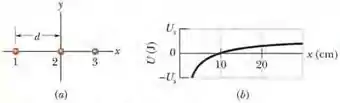
Passo 1
Vamos tentar tirar alguma informação da figura (b). O gráfico da energia cruza o eixo x em 10 cm. Isso significa que quando a partícula 3 está em x = 10 cm, a energia é zero.
Passo 2
Pegue a fórmula da energia potencial do sistema quando a partícula 3 está em x = 10 cm e iguale a 0:
Passo 3
Agora isolamos :
Substituindo os valores dados de , e , obtemos