Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 23.Exercício - Ex. 50
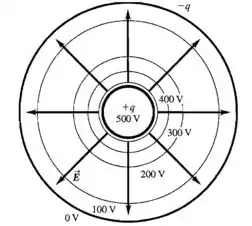
Uma esfera metálica com raio está apoiada sobre uma base isolada no centro de uma casca esférica metálica com raio externo . Existe uma carga +q na esfera interna e uma carga -q na esfera externa. O módulo de q é escolhido para produzir uma diferença de potencial entre as esferas igual a 500V, mantendo a esfera interna com um potencial mais elevado.
a)Use para calcular o valor de q.
b)Com base nas expressões : , e , faça um desenho indicando as superfícies equipotenciais que correspondem a 500, 400, 300, 200, 100 e 0 V.
c)Sobre o seu desenho, mostre as linhas de campo elétrico. As linhas de campo elétrico e as superfícies equipotenciais são mutuamente perpendiculares? A superfícies equipotenciais ficam mais próximas entre si quando o módulo de E é mais elevado?
Passo 1
letra a)
Precisamos calcular q a partir da expressão:
Isolando o q:
Passo 2
letra b)
Para fazermos o desenho das superfícies equipotenciais, precisamos calcular as posições onde temos os potenciais dados.
Vamos pegar a relação:
Como na superfície da esfera mais externa o potencial é nulo: para
Isolando o r temos:
Passo 3
Agora precisamos substituir os potenciais para achar as distâncias:
Passo 4
Desenhando as superfícies equipotenciais com as distâncias calculadas no passo anterior:
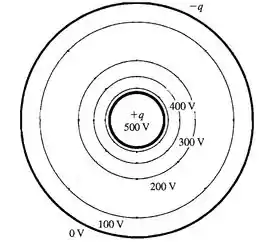
Passo 5
letra c)
O campo elétrico tem direção radial e como a carga é positiva ele aponta para fora. Então temos:
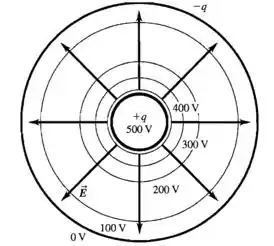
Passo 6
As superfícies equipotenciais e as linhas de campo elétrico são perpendiculares.
Além disso, as superfícies equipotenciais estão mais juntas próximo do centro, onde o campo elétrico é mais intenso.
Resposta
letra a)
letra b)
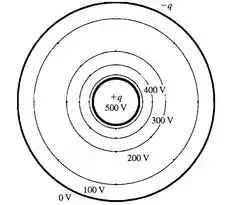
letra c) São perpendiculares. Sim, ficam.
