Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 39
- A FIGURA P11.39a representa a força exercida sobre uma partícula que se move ao longo do eixo . Desenhe o gráfico da energia potencial da partícula em função da posição x. Considere que em .
- b. A FIGURA P11.39b representa a energia potencial de uma partícula que se move ao longo do eixo . Desenhe o gráfico da força em função da posição .
Passo 1
Para esse tipo de matéria devemos ter no sangue que:
Então como na letra queremos o gráfico da energia potencial em relação a posição então:
Onde a força da letra pode ser entendida como uma função composta:
Nessa segunda é simples pois temos uma reta onde em e .
Então a energia potencial nessa função será de:
Onde na primeira parte da função se aplicarmos , nós teremos , portanto .
Então para e para essa primeira parcela da função terá , portanto a segunda parcela da função ficará como:
Pois os dois gráficos tem que se encontrar em um ponto, tal como na função .
Logo a função da energia potencial fica:
Plotando um gráfico dessa função composta nós teremos:
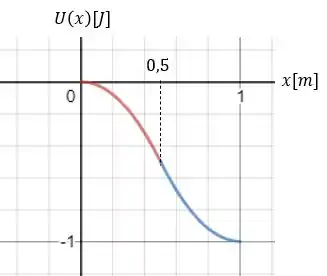
Passo 2
E como na letra queremos o gráfico de então:
No intervalo entre teremos uma força constante de:
E no intervalo entre e teremos:
Nos dando um gráfico igual a:
