Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.3 - Ex. 31
Suponha que o trenó do Exercício 6.30 esteja inicialmente em repouso em . Use o teorema do trabalho-energia para achar a velocidade do trenó em:
a) ;
b) .
Despreze o atrito entre o trenó e a superfície do lago.
Passo 1
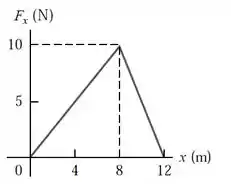
Opa, bora lá! O enunciado nos dá um gráfico de força versus comprimento de um trenó deslizando no gelo e nos pede pra a gente calcular a velocidade final do trenó:
A massa do trenó é e também devemos ignorar o atrito entre a superfície do lago e do trenó.
Devemos usar o teorema de trabalho-energia. O que diz esse teorema? Ele diz
Onde é a energia cinética. E podemos calcular por:
Se o trenó estava em repouso, isso quer dizer que a energia cinética inicial é zero (pois ). A energia cinética final vai estar associada à velocidade do trenó no final do deslocamento indicado e vai valer
Temos então:
Como a gente faz para achar esse trabalho total? Então, ele nos deu um gráfico de como a força varia com o deslocamento. O trabalho até certo ponto vai ser área sob esse gráfico até esse ponto.
Então que a gente precisa fazer é calcular a área do gráfico até o ponto onde ele pede a velocidade.
Agora vamos aplicar para os casos que se pede.
Passo 2
- A área abaixo do gráfico até é um triângulo
- A área abaixo do gráfico até é um triângulo,
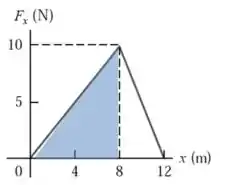
Então podemos fazer
O trabalho realizado entre e é então , a massa do trenó é e substituindo na expressão que deduzi ali em cima podemos achar a velocidade:
Passo 3
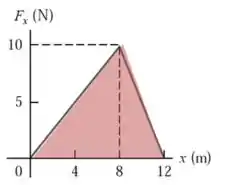
Então podemos fazer
Do mesmo modo, o trabalho realizado entre e é , a massa do trenó continua sendo e substituindo na expressão podemos achar a velocidade
Prontinho!