Seja e
- Desenhe um sistema de coordenadas e sobre ele represente os vetores e .
- Efetue a subtração gráfica para obter
Passo 1
- Desenhe um sistema de coordenadas e sobre ele represente os vetores e .
- Efetue a subtração gráfica para obter
Para desenharmos os vetores em um plano cartesiano precisamos saber quais são as componentes e desses vetores. A questão nos dá essas informações, saca só:
Os vetores unitários , , são vetores que indicam a direção dos eixos e , respectivamente, no plano cartesiano. Então, se eu digo que um vetor , eu quero dizer que sua componente no eixo , , vale 2 e sua componente no eixo , , vale 4, certo?
Sabendo disso, temos para o vetor
E para o vetor
Agora podemos desenhar esses vetores no plano cartesiano:
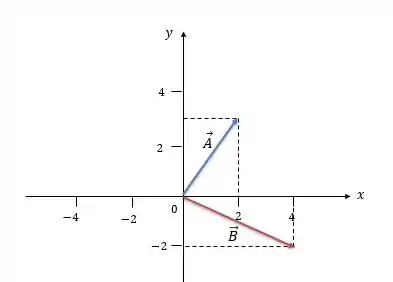
Passo 2
A gente pode reescrever essa subtração como uma soma, saca só:
E seguir o passo a passo para achar a soma de dois vetores:
- Desenhe o vetor ;
- Desenho o vetor com a cauda na pontinha do vetor ;
- Desenhe uma seta que começa na calda de e termina na pontinha de . Esse é o vetor soma.
Mas antes, precisamos saber quem é o vetor .
O sinal de menos ou mais em um vetor indica o sentido do vetor. Esse sinal de menos no vetor quer dizer justamente que o vetor está no sentido contrário. Então, o vetor é o vetor mas com sentido contrário.
Desse jeito aqui óh:
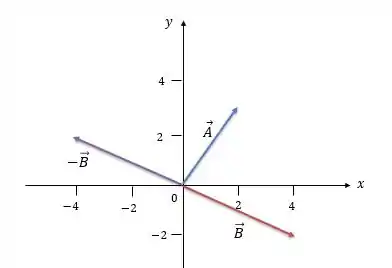
Passo 2
Agora que sabemos quem é o vetor vamos seguir as regrinhas:
Primeiro vamos desenhar o vetor e o vetor com a calda na pontinha do vetor :
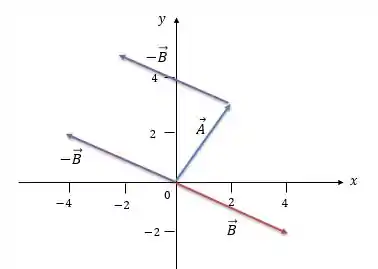
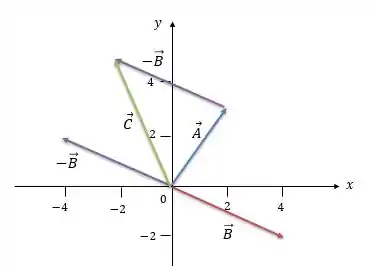
Agora vamos fazer a seta, ligando a calda do vetor com a pontinha do vetor :
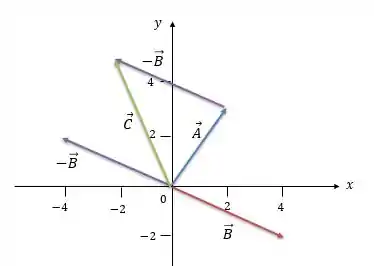
Prontinho, o vetor em verde é o nosso vetor
Resposta