Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.7 - Ex. 58
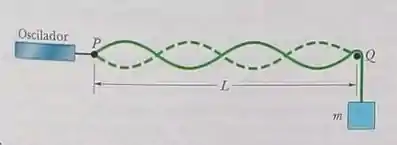
Na figura, uma corda, presa a um oscilador senoidal no ponto e apoiada em um suporte no ponto , é tensionada por um bloco de massa . A distância entre e é , a massa específica linear da corda é e a frequência do oscilador é . A amplitude do deslocamento do ponto é suficientemente pequena para que esse ponto seja considerado um nó. Também existe um nó no ponto . (a) Qual deve ser o valor da massa para que o oscilador produza na corda o quarto harmônico? (b) Qual é o modo produzido na corda pelo oscilador para ?
Passo 1
- Aqui, a gente precisa lembrar do que significa um n-ésimo harmônico. Sendo o comprimento da corda e o comprimento de onda da onda estacionária, quando uma corda está fixa em ambas as extremidades acontece isso aqui:
Passo 2
Beleza! Agora, vamos exercitar mais um pouco a memória e lembrar que
Em que e são a tensão na corda e a sua densidade linear. Além disso, a gente também sabe que . Juntando essas duas relações, e a do passo 1 (), vem:
Disso, isolando , a gente obtém essa relação bonita aqui:
Nesse caso, sendo o peso do bloco.
Passo 3
Pronto! Agora bora isolar na equação acima! Fazendo isso, a gente obtém isso:
No quarto harmônico acontece que . Então:
Passo 4
(b)Se , então o valor de correspondente é (usando o fato de que ):
Como esse valor não é inteiro, essa massa de não vai ser capaz de criar um modo estacionário de vibração da corda.
Resposta
- Nenhum