A força de arrasto em uma esfera em movimento a um nível muito baixo de número de Reynolds é dado por , onde está a viscosidade do fluido circundante e é o raio da esfera. (Essa relação é chamada Lei de Stokes.) Usando essas informações, encontre a velocidade terminal da subida para uma bolha esférica de dióxido de carbono com 1,0 mm de diâmetro subindo em uma bebida carbonatada ( e ). Quão mais deve demorar para que essa bolha suba 20 cm (a altura da bebida vidro)? Esse período de tempo é consistente com suas observações?
Passo 1
Vamos tentar imaginar a situação na qual a bolha esférica se encontra. Note que há três forças presentes na bolha.
1ª) Força flutuante na bolha, dada pelo princípio de Arquimedes.
2ª) Força peso, massa vezes a gravidade
3ª) Força de arrasto
A imagem abaixo pode facilitar ainda mais a visualização do que acontece na bolha.
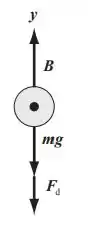
Passo 2
Lembra da segunda Lei de Neto, que afirma:
Vamos utilizar para acharmos uma relação entre as forças, desse modo,
Onde, , é a massa do gás.
Como a velocidade de princípio é constante a aceleração é igual a 0. Portanto,
Vamos guardar por enquanto essa equação.
Passo 3
Como dito anteriormente, B é a força flutuante, que é dada pelo princípio de Arquimedes:
Onde:
massa do fluido
volume da bolha
densidade do refrigerante
Também podemos expressar a massa, , em função da sua densidade. Com isso,
Passo 4
Substituindo as equações que achamos, na equação que relaciona as forças
Isolando a velocidade temos,
Podemos fazer essa aproximação, pois a densidade no refrigerante é muito mais que a densidade do gás.
Passo 5
Estamos quase lá. Agora vamos substituir os valores para acharmos a velocidade, sabendo a velocidade, temos a altura, podemos achar o tempo.
Como,
Observe que, o tempo parece razoável com o que observamos no dia a dia.
Resposta
0,6 s