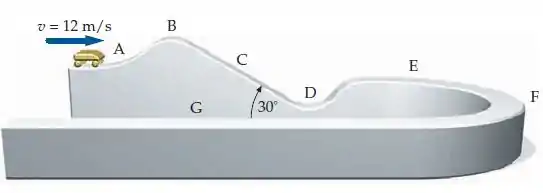
Sua firma está projetando uma nova montanha-russa. Para a concessão do alvará de funcionamento, é exigido o cálculo de forças e de acelerações em vários pontos importantes do percurso. Cada carrinho terá uma massa total (incluindo a dos passageiros) de e viajará livremente sobre o trilho sinuoso sem atrito mostrado na figura. Os pontos , e estão em trechos retos horizontais, todos à mesma altura de acima do solo. O ponto está a uma altura de acima do solo em um trecho inclinado de . O ponto está na crista de uma elevação, enquanto o ponto está no nível do solo, no fundo de um vale. O raio de curvatura nestes dois pontos é de . O ponto está no meio de uma curva horizontal de perfil inclinado, com um raio de curvatura de , e à mesma altura dos pontos , e . No ponto , a rapidez do carrinho é . (a) Se o carrinho tem justo as mínimas condições para vencer a barreira no ponto , qual deve ser a altura do ponto em relação ao solo? (b) Se o carrinho tem justo as mínimas condições para vencer a barreira no ponto , qual deve ser a magnitude da força exercida pelo trilho sobre o carrinho nesse ponto? (c) Qual será a aceleração do carrinho no ponto ? (d) Quais serão a magnitude e a orientação da força exercida pelo trilho sobre o carrinho no ponto ? (e) Quais serão a magnitude e a orientação da força exercida pelo trilho sobre o carrinho, no ponto ? (f) Em , uma força constante de frenagem é aplicada ao carrinho devendo fazer com que ele páre após . Qual é a magnitude que deve ter essa força?

(b) Se o carrinho tem apenas as condições mínimas para vencer a barreira, isso significa que ele chega ao ponto com .

Nesse caso, a única força que o trilho exerce sobre o carrinho é a força normal. Como o ponto está na crista da elevação, ele está em um trecho horizontal, e então:

E então a força que o trilho exerce sobre o carrinho é:

(c) A aceleração do carrinho no ponto será paralela ao plano inclinado naquele trecho. Vamos aplicar a segunda lei de Newton nessa direção:

E substituindo os valores numéricos:

(d) No ponto , as forças que o trilho exerce sobre o carrinho são todas verticais. Primeiro vamos calcular a rapidez com que o carrinho passa por esse ponto.

No ponto , tínhamos rapidez nula e uma altura em relação ao solo. Segundo o enunciado, o ponto está na altura do solo, então . Aplicando a conservação de energia entre esses dois pontos ficamos com o seguinte resultado:

E como a força resultante sobre o carrinho em precisa cumprir o papel de força centrípeta, temos que:

Então a força que o trilho exerce sobre o carrinho na direção vertical para cima é:

E substituindo os valores numéricos:

(e) Vamos começar calculando a rapidez do carrinho em , que está a uma altura de m em relação ao solo.

Podemos aplicar a conservação de energia entre e para encontrar :

E agora podemos calcular a força centrípeta que o trilho precisa exercer sobre o carrinho em , na direção horizontal para a esquerda, para mantê-lo na trajetória circular mostrada na figura:

Substituindo os valores numéricos:

Além disso, o trilho também exerce uma força normal sobre o carrinho em . Como esse ponto está sobre um trecho horizontal, essa força normal é:

E aponta na vertical para cima. Portanto temos uma força vertical de magnitude e uma horizontal de magnitude , então a resultante é:

E para definir a orientação dessa força, vamos encontrar o ângulo que ela forma com a horizontal:

(f) A rapidez do carrinho em é necessariamente a mesma que tínhamos em , então:

Para que a força de frenagem pare o carro em , o trabalho realizado por esa força ao longo dessa distância deve ser igual à energia cinética que o carrinho tem ao cruzar o ponto :

E substituindo os valores numéricos: