Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 35
|| O Frisbee de seu amigo ficou preso em uma árvore a acima do solo. Você deseja desalojá-lo acertando-o com uma pedra. O brinquedo está firmemente preso à árvore, de modo que você percebe que a pedra precisa estar se deslocando com velocidade de,
no mínimo, ao bater no Frisbee.
O valor da velocidade de arremesso da pedra depende do ângulo segundo o qual ela é arremessada? Explique.
Se a pedra for liberada a 2,0 m acima do solo, com que valor mínimo de velocidade você deverá arremessá-la?
Passo 1
Um esquema é:
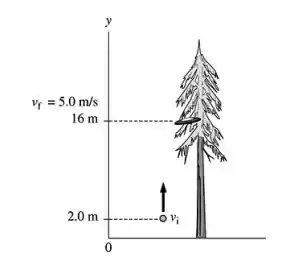
Passo 2
Podemos usar o princípio da conservação de energia mecânica e mudar os dados conforme necessidade:
Mas, em mecânica:
Assim:
Então:
Mas podemos por o em evidencia em ambos os lados e simplifica-lo.
Passo 3
O valor da velocidade de arremesso da pedra depende do ângulo segundo o qual ela é arremessada? Explique.
Não depende.
Veja que a fórmula anterior, não dependemos de nenhum ângulo. Só dependemos da velocidade, gravidade e altura!
Se a pedra for liberada a 2,0 m acima do solo, com que valor mínimo de velocidade você deverá arremessá-la?
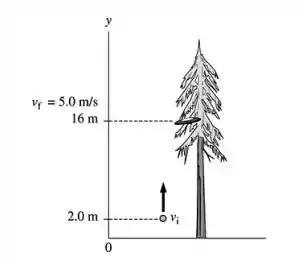
Substituindo os termos na fórmula do passo 2:
Esse é o valor de velocidade inicial mínima que vc deve lançar.
Resposta
Não depende de nenhum ângulo.
Pela dedução vê-se que dependemos da velocidade, gravidade e altura!