Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 57

Uma firma de propaganda contatou sua firma de engenharia para criar um novo anúncio para uma sorveteria. O proprietário desta sorveteria deseja adicionar cones sólidos girantes (pintados de maneira a parecerem cones de sorvete, obviamente) para chamar a atenção dos passantes. Cada cone deverá girar em torno de um eixo paralelo à sua base a passando pelo seu vértice. O tamanho real dos cones é para ser decidido, e o proprietário pergunta se é mais eficiente, do ponto de vista energético, fazer girar cones menores ou cones maiores. Ele solicita à sua firma um relatório escrito, mostrando a determinação do momento de inercia de um cone circular reto homogêneo de altura H , raio da base R e massa M . Qual é o resultado de seu relatório?

Passo 1

Bora lá. A gente quer resolver um problema parecido com o 56, mas agora queremos o momento de inércia em relação ao eixo x .

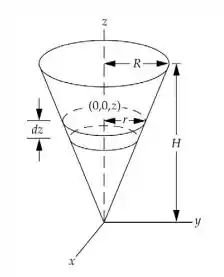
Pra isso, vamos usar o teorema dos eixos paralelos. Lembra também que o raio pode ser calculado por semelhança de triângulos, e a massa é d m = ρ d V = ρ π r 2 d z .

Passo 2

Teorema dos eixos paralelos:

d I x = d I d i s c o + d m z 2

d I x = d I d i s c o +   ρ π r 2 z 2 d z

No problema 56 nós calculamos o momento de inércia de inércia de um disco fino de massa M e raio R, rodando ao redor do diâmetro, e achamos I = 1 4 M R 2 . Confere lá!

Para o nosso disco, então, I = 1 4 m r 2 .

d I = 1 4 d m r 2 = 1 4 ρ π r 2 d z r 2 = 1 4 ρ π r 4 d z

Da semelhança de triângulos:

r z = R H → r = R H z

d I d i s c o = 1 4 ρ π R H z 4 d z

Substituindo no teorema:

d I x = 1 4 ρ π R H z 4 d z +   ρ π r 2 z 2 d z

d I x = 1 4 ρ π R H 4 z 4 d z +   ρ π R H z 2 z 2 d z

d I x = 1 4 ρ π R H 4 z 4 d z +   ρ π R H 2 z 4 d z

Integrando de 0 a H:

I x = ∫ 0 H 1 4 ρ π R H 4 z 4 d z +   ρ π R H 2 z 4 d z

I x = ∫ 0 H 1 4 ρ π R H 4 z 4 d z + ∫ 0 H ρ π R H 2 z 4 d z

I x = π ρ R 4 4 H 4 × H 5 5 + ρ π R 2 H 2 × H 5 5

I x = π ρ R 4 H 20 + R 2 H 3 5

Passo 3

A massa do cone pode ser calculada em função da massinha do disco:

M = π ρ ∫ 0 H r 2 d = π ρ ∫ 0 H R 2 H 2 z 2 d z

M = 1 3 π ρ R 2 H

Dividindo I x por M, vamos obter:

I x = 3 M H 2 5 + R 2 20

Resposta

I x = 3 M H 2 5 + R 2 20

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pião cônico homogêneo de massa M tem raio da base R e altura h . (a) Calcule a posição do centro de massa do pião. (b) Com o auxilio do resultado do probl. 5, calcule a velocidade angular Ω de prec
Calcule o momento de inércia de uma lamina homogênea de massa M em forma de anel circular de raio interno r 1 e raio externo r 2 , (a) Em relação a um eixo perpendicular ao plano do anel, passadno pel
Como aplicação do teorema dos eixos perpendiculares (Probl. 1), calcule: (a) O momento de inércia para uma placa retangular homohenea de massa M e lados a e b em relação a um eixo perpendicular a seu
O teto da sala de jantar dos estudantes da sua faculdade será apoiado por vigas de madeira cruzadas altas fixadas na forma de um L de cabeça para baixo (Figura 9-73). Cada membro vertical tem 10,0 pés
A molécula de oxigênio ( O 2 ) tem uma massa de 5,30 × 10 - 26k g e um momento de inércia de 1,94.10 - 46k g ∙ m 2 em relação a um eixo que passa pelo ponto médio da reta que liga os dois átomos e é p