Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 118
O teto da sala de jantar dos estudantes da sua faculdade será apoiado por vigas de madeira cruzadas altas fixadas na forma de um L de cabeça para baixo (Figura 9-73). Cada membro vertical tem 10,0 pés de altura e 2,0 pés de largura, e o membro transversal horizontal tem 8,0 pés de comprimento. A massa da viga vertical é de 350 kg e a massa da viga horizontal é de 280 kg. Enquanto os trabalhadores construíam o salão, uma dessas estruturas começou a cair antes de ser ancorada no lugar. (Felizmente, eles o pararam antes que caísse.) (A) Se ele começou a cair da posição vertical, qual foi a aceleração angular inicial da estrutura? Suponha que o fundo não deslize pelo chão e não caia fora do plano, ou seja, que durante a queda a estrutura permaneça no plano vertical definido pela posição inicial da estrutura. (b) Qual seria a magnitude da aceleração linear inicial do canto superior direito da viga horizontal? (c) Qual seria o componente horizontal da aceleração linear inicial nesse mesmo local? (d) Estimar a velocidade de rotação da estrutura no impacto
Passo 1
(a) A estrutura ao cair, irá rotacionar em torno da quina da viga vertical, no ponto P da imagem:
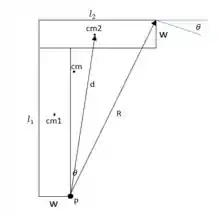
Vamos chamar a viga horizontal de 2 e a vertical de 1. Como os lados menores de cada viga que compõe a estrutura são iguais, chamaremos eles de w e os lados maiores serão e . Escrevemos então a segunda lei de Newton para o torque para o conjunto composto pelas duas vigas:
Como o centro de massa de cada viga se encontra no centro delas, os torques para cada uma serão (a gravidade irá atuar no centro de massa):
Isolando :
Passo 2
Vamos agora encontrar os momentos de inercia de cada viga em relação ao ponto P:
Utilizando a tabela 9-1 do livro e o teorema dos eixos paralelos escrevemos os momentos de inércia da seguinte maneira:
Substituindo valores numéricos:
E para :
Sendo (mostrado na figura):
E da mesma tabela 9-1 temos:
E será:
Substituindo valores numéricos:
A aceleração angular será então:
Substituindo valores:
Passo 3
Na letra (b), precisaremos utilizar o R da imagem, que é a distância do ponto P do eixo de rotação até o ponto que o enunciado pede:
E a aceleração linear do ponto é:
Sendo a aceleração angular encontrada no passo anterior, ficamos então com:
Substituindo o valor de cada grandeza:
Passo 4
A (c) nos pede a componente x da aceleração linear do mesmo ponto, para isso vamos utilizar o ângulo formado entre a viga vertical e a distância R, chamaremos ele de . E através de poucos cálculos por triângulos, podemos dizer que o ângulo do ponto também é , como na figura do Passo 1, então:
E substituindo o cosseno:
Substituindo valores numéricos:
Passo 5
Bom na letra (d), vamos precisar usar o princípio de conservação de energia:
Vamos colocar o zero do potencial gravitacional exatamente na altura do centro de massa exatamente quando a estrutura está prestes a atingir o solo, portanto, , e como no início da queda , ficamos com:
Como estamos utilizando a altura do centro de massa para resolvermos o problema, a energia potencial inicial será escrita em termos da diferença de altura entre a altura inicial do centro de massa e a altura final:
As energias então serão:
Isolando :
Passo 6
Precisamos agora determinar
A altura do centro de massa antes da estrutura cair será soma da posição do centro de massa de cada corpo vezes sua massa sobre a massa total:
Substituindo valores numéricos:
E para a altura final escrevemos:
Onde as duas alturas correspondem às alturas dos centros de massa de cada viga, para escrevê-las, vamos precisar considerar os seguintes esquemas, para a viga 1 depois de cair:
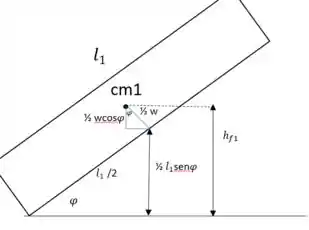
Podemos então mostrar que:
E para a viga 2:
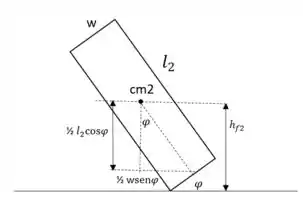
Mostramos também:
Substituindo os dois resultados na altura final do centro de massa:
Sabendo que podemos substituir valores numéricos para cada grandeza:
Passo 7
E então substituímos na equação de
Por fim, substituindo na equação da velocidade angular: