Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 59

Um cilindro de 2,5 k g , cujo raio é de 11 c m , inicialmente em repouso, pode girar livremente em torno de seu eixo. Uma corda de massa desprezível é enrolada em torno dele e puxada com uma força de 17 N . Supondo que a corda não escorregue, determine (a) o torque exercido pela corda sobre o cilindro, (b) a aceleração angular do cilindro e (c) a rapidez angular do cilindro após 0,50 s .

Passo 1

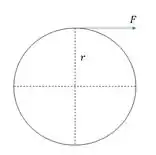
  1. Pra achar o torque, é só a gente usar a definição:

    2. τ = F × r = 17 N × 0.11 m

    τ = 1.87   N ⋅ m

    Passo 2

  2. Relacionamos o torque à aceleração angular pela fórmula:

    3. τ = I α

    Para o cilindro, I = 1 2 M R 2 . Então, substituindo:

    α = 2 τ M R 2

    α = 2 × 1.87 2.5 × 0.11 2 = 124 r a d s 2

    α = 1.24 × 10 2 r a d s 2

    Passo 3

  3. Agora, pra terminar, é só relacionar a velocidade angular com a aceleração!

ω = ω 0 + α t

Como o cilindro começou parado, ω 0 = 0 .

ω = α t = 124 r a d s 2 0.50 s

ω = 62 r a d s

Resposta

τ = 1.87   N ⋅ m

α = 1.24 × 10 2 r a d s 2

ω = 62 r a d s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quatro partículas, todas de massa m = 0,2 k g , ocupam os vértices de um quadrado com l = 0,5 m de lado. As partículas estão ligadas por uma barra de massa desprezível. Este corpo rígido pode girar em
Uma pá do rotor de um helicóptero é homogênea, tem 7,80m de comprimento, urna massa de 110k g e está presa ao eixo do rotor por um único parafuso. (a) Qual é o módulo da força exercida pelo eixo sobre
Duas esferas homogêneas maciças têm a mesma massa de 1,65k g , mas o raio de uma é 0 , 226m e o da outra é 0,854m . Ambas p o dem girar em tomo de um eixo que passa pelo centro. (a) Qual é o módulo T
Um equilibrista procura manter sempre seu centro de massa verticalmente acima do arame (ou corda). Para isso, carrega muitas vezes uma vara comprida. Quando se inclina, digamos, para a direita (desloc
N a Fig. 10-52, uma roda com 0,20m de raio é montada em um eixo horizontal sem atrito. Uma corda de massa desprezível é enrolada na roda e presa a uma caixa de 2,0k g que escorrega sobre uma superfíci