Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.5 - Ex. 42
Um flutuador tem a forma de um cilindro reto,com de altura e de área das bases; sua massa específica é vezes a massa específica da água doce. Inicialmente o flutuador é mantido totalmente imerso em água doce, com a face superior na superfície da água. Em seguida é liberado e sobe gradualmente até começar a flutuar. Qual é o trabalho realizado pelo empuxo sobre o flutuador durante a subida?
Passo 1
Fala galerinha bonita, tudo beleza?
Nesse exercício aqui, queremos calcular o trabalho realizado pelo empuxo. Então vamos lembrar que o trabalho de uma força é dado como:
Onde representa o deslocamento exercido pela força.
Como queremos do empuxo:
E, lembrando que :
Sabemos tanto o quanto o , pois o fluido é a água. Então, precisamos saber o .
Como , onde está representando a altura submersa do cilindro, agora:
Então, na verdade, precisamos saber o quanto essa altura submersa variou! Vem comigo, então!
Passo 2
Primeiramente, vamos analisar o que acontece com o Empuxo durante o processo de subida do flutuador. Inicialmente, temos o flutuador completamente submerso, estando com sua face superior na superfície da água. Com isso, temos duas forças agindo sobre ele: empuxo () e peso ().
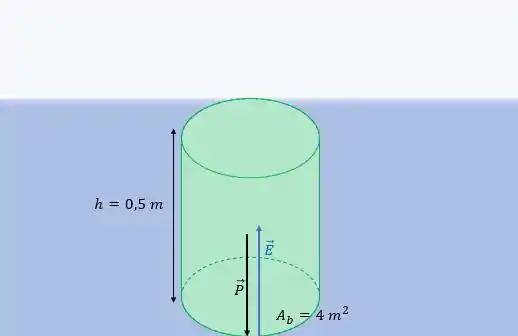
O flutuador vai subir até o empuxo e a força peso estarem em equilíbrio, dessa forma, elas se anulam e o objeto fica apenas boiando na água. Então, no fim do dia, teremos uma situação mais ou menos assim:
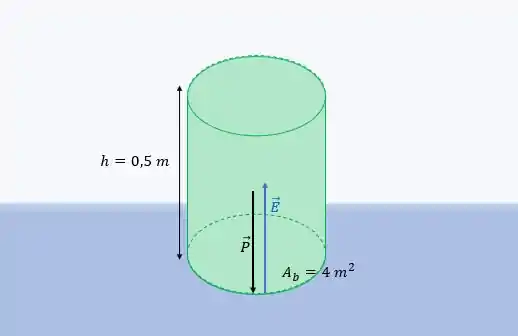
Show? Então, repare que, conforme o flutuador sobe, ele fica cada vez menos submerso, certo?? Ou seja, seu volume submerso vai diminuindo! E isso tem uma importante relação com o empuxo sobre o flutuador. Isso porque o empuxo pode ser calculado por:
Então, como o diminui conforme o flutuador sobe, o empuxo também vai diminuindo gradualmente, já que eles são diretamente proporcionais. E isso acontece até o empuxo se igualar ao peso do cilindro, como vemos na segunda imagem. Ou seja, o flutuador sobe até que:
Cortando :
Em que é a massa do flutuador cilíndrico.
Passo 3
Iradoso, agora como a densidade é dada por:
Então isolando :
Mas agora, vamos usar a massa do flutuador, o volume do flutuador e a massa específica também, ok? Então:
A expressão para a massa do passo anterior fica assim, tínhamos:
Substituindo que acabamos de encontrar:
Então, sendo a área da base do flutuador, sua altura total e a altura da parte submersa do flutuador, temos que:
E
Então, a expressão acima pode ser escrita assim:
Podemos cortar :
Dessa forma, achamos uma expressão para :
Passo 4
Show! Com essa expressão:
Lembrando que o enunciado nos diz . Podemos substituir os valores fornecidos no enunciado, e teremos:
Como o flutuador tem de altura:
Passo 5
Agora, podemos calcular o trabalho efetuado pela força de empuxo . Como vimos láaa no primeiro passo:
Onde é a altura submersa do cilindro.
Como a altura submersa saiu de , quando o cilindro inteiro estava dentro da água, para , quando o cilindro estava em equilíbrio:
Como , e :
Podemos tirar o resultado dessa multiplicação da integral, por ser constante:
Resolvendo a integral acima, vamos obter:
Calma, esse sinal negativo só apareceu por causa do nosso referencial, eu coloquei que a profundidade aumenta para baixo e o empuxo aponta para cima! Isso não diz muita coisa nesse exercício. Como o problema só quer o valor do trabalho realizado, podemos pegar o módulo desse trabalho, sendo assim: