Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.9 - Ex. 48

Uma fonte alternada de frequência variável f d é ligada em série com um resistor de 8 0,0   Ω e um indutor de 4 0,0   m H . A amplitude da força eletromotriz é 6 , 0 0   V . (a) Desenhe um diagrama fasorial para o fasor V R (tensão no resistor) e para o fasor V L (tensão no indutor). (b) Para que a frequência de excitação f d os dois fasores tem o mesmo comprimento? Para essa frequência, determine (c) o ângulo de fase em graus, (d) a velocidade angular de rotação dos fasores e (e) a amplitude da corrente.

Passo 1

A questão trata de um circuito R L com corrente alternada. No item (a) é pedido para fazermos um diagrama de fasores. Para isso, basta lembrar que a tensão no indutor está 90 ° adiantada com relação a corrente (tensão no resistor). Assim, o diagrama é do tipo:

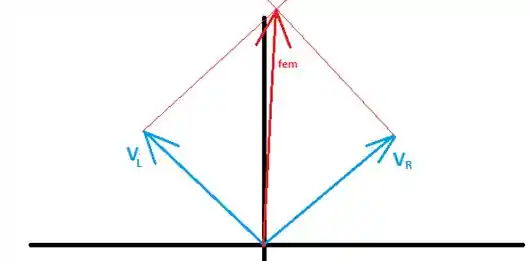
Note que

ε 2 = V R 2 + V L 2

Passo 2

Para o item (b), temos que lembrar que V R = R I e V L = χ L I . Assim, para que os fasores tenham o mesmo comprimento:

V R = V L ⇒ R = χ L

Assim,

R = ω d L ⇒ ω d = R L

Portanto, com R = 8 0,0   Ω e L = 40,0 ⋅ 10 - 3   H :

ω d = 2 000   r a d / s

Essa é a velocidade angular dos fasores (respondemos o item (d)). Para achar a frequência:

f d = ω d 2 π

Assim,

f d = 318   H z

Passo 3

A fase é dada por

tan ⁡ ϕ = χ L - χ C R

Neste caso, χ C = 0 , de modo que

tan ⁡ ϕ = χ L R = ω d L R

Mas temos que para essa frequência:

ω d L = R ⇒ ω d L R = 1

Assim,

tan ⁡ ϕ = 1 ⇒ ϕ = 45 °

Passo 4

Por fim, a amplitude da corrente será

I = ε Z = ε R 2 + χ L 2

Assim,

I = ε R 2 + ω d L 2 = ε R 2 + R 2 = ε R 2

Substituindo os números:

I = 0 , 053   A

Resposta

f d = 318   H z

ϕ = 45 °

ω d = 2000   r a d / s

I = 0 , 053   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Remova o capacitor do circuito da Fig. 31-7 e faça R = 200Ω , L = 230m H , f d = 60 , 0H z e ε M = 36,0V . Determine o valor (a) de Z ; (b) de ϕ ; (c) de I . (d) Desenhe um diagrama fasorial.
A Fig. 31-29 mostra a amplitude I da corrente em função da frequência angular de excitação ω d de um circuito R L C . A escala de eixo vertical é definida por I s = 4,00A . A indutância é 200μ H e a a
Uma fonte de corrente alternada de frequência variável, um indutor de indutância L e um resistor de resistência R são ligados em série. A Fig. 31-30 mostra a impedância Z do circuito em função da freq
Remova o indutor do circuito da Fig. 31-7 e faça R = 200Ω , C = 15,0μ F , f d = 60 , 0H z e ε M = 36,0V . Determine o valor (a) de Z ; (b) de ϕ ; (c) de I . (d) Desenhe um diagrama fasorial.
Na Fig. 31-7, faça R = 200Ω , C = 70 , 0μ F , L = 230m H , f d = 60,0H z e ε M = 36,0V . Determine o valor (a) de Z ; (b) de ϕ ; (c) de I . (d) Desenhe um diagrama fasorial.