Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.9 - Ex. 38
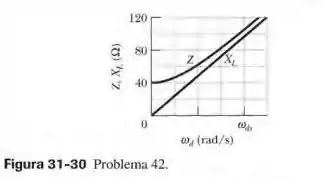
Uma fonte de corrente alternada de frequência variável, um indutor de indutância e um resistor de resistência são ligados em série. A Fig. 31-30 mostra a impedância do circuito em função da frequência de excitação com a escala do eixo horizontal definida por . A figura mostra também a reatância do indutor em função de . Determine o valor (a) de e (b) de .
Passo 1
Bom, o problema diz que os únicos elementos do circuito, além da fonte, são o indutor e o resistor. Assim, temos um circuito com . Portanto,
Sabemos também que
Assim, para , temos que , de modo que
Vemos que para , temos que , de modo que
Passo 2
Agora, para achar note que
Assim, escolhendo um ponto do gráfico e , temos que
Resposta
Exercícios de Livros Relacionados
11. Capacitância na cozinha. O circuito de um refrigerador contém um capacitor na entrada. Uma voltagem com amplitude de 170V e frequência igual a 60H z é aplicada através do capacitor e produz uma co
06. Uma capacitância C e uma indutância L são operadas na mesma frequência angular. ( a ) Em qual frequência angular elas terão a mesma reatância? ( b ) Se L = 5,0m H e C = 3,50μ F , qual é o valor nu
09. ( a ) Calcule a reatância de um indutor de 3,0H para uma frequência de 80H z ? ( b ) Qual a indutância de um indutor cuja reatância é igual a 120Ω para 80,0H z ? ( c ) Calcule a reatância de um ca
08. ( a ) Calcule a reatância de um indutor de 0,450H para frequências de 60H z e 600H z . ( b ) Calcule a reatância de um capacitor de 2,50μ F para as mesmas frequências. ( c ) Para qual frequência a
04. Um capacitor de 2,20μ F está conectado através de uma fonte c a cuja amplitude da voltagem é mantida constante a 60,0V , mas cuja frequência pode variar. Calcule a amplitude da corrente para quand