Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Exercício - Ex. 04
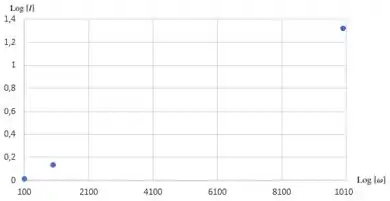
04. Um capacitor de está conectado através de uma fonte cuja amplitude da voltagem é mantida constante a , mas cuja frequência pode variar. Calcule a amplitude da corrente para quando a frequência angular for: ; ; . Mostre os resultados de até fazendo um gráfico de contra .
Passo 1
Antes de começar a resolução preciso dizer que há um erro no enunciado (provavelmente da tradução), nele diz que a amplitude de corrente é mantida constante a mas na verdade era para estar escrito que a amplitude de VOLTAGEM é . Amplitude de corrente é o que a gente quer. Então, dito isso, podemos começar.
Essa questão nos pede a amplitude da corrente para diferentes frequências angulares que nos foram dadas.
O enunciado nos dá também a capacitância do capacitor e a amplitude de voltagem . Ou seja, vamos precisar utilizar equações que as relacionam.
Como nós temos um capacitor usaremos as equações que são mostradas na página do nosso livro.
A Equação nos diz que:
Enquanto a equação que nos diz que a reatância capacitiva é:
Então:
Ah, mais uma coisinha importante é que capacitância que nos foi dada foi:
Que é a mesma coisa que:
Prontinho, temos o que é necessário para fazer a questão. Agora mãos à obra!
Passo 2
Para .
Substituindo tudo o que temos na equação que chegamos no Passo 1:
Agora é só repetir em e mudando o .
Passo 3
Para .
Passo 4
Para .
Passo 5
Sendo temos que e são constantes, e e são variáveis, onde depende de .
Sendo assim podemos dizer que:
Resposta
