Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.Problemas Adicionais - Ex. 86
Uma fonte sonora se move ao longo de um eixo , entre os detectores e . O comprimento de onda do som detectado por é do comprimento do som detectado por . Qual é a razão entre a velocidade da fonte e a velocidade do som?
Passo 1
Vamos admitir que a fonte se desloque no sentido de para conforme o esquema abaixo:
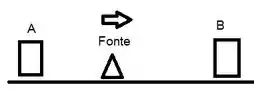
A frequência detectada tanto por , quanto por está defasada por conta do efeito Doppler. Vamos determinar primeiro as frequências por eles detectadas.
Para o detector :
A fonte está se afastanto do observador, logo a velocidade tem sinal positivo. Como o detector está em repouso, a velocidade do observador é nulo. Pela fórmula do efeito Doppler temos:
E, sabendo que tanto para o detector , quanto para o a frequência emitida pela fonte é a mesma, já vou deixar isolado para poder fazer a comparação nos próximos passos.
Assim temos:
Passo 2
Do ponto de vista do detector , a fonte está de aproximando, então o sinal da velocidade é negativo. O observador está em repouso, então . A frequência detectada em é:
Assim podemos isolar a frequência da fonte:
Passo 3
Agora vamos usar o fato de que a frequência emitida pela fonte é a mesma para os dois detectores, então:
E sabendo que , então temos:
E também que , podemos simplificar a expressão acima: