Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 7.3 - Ex. 6
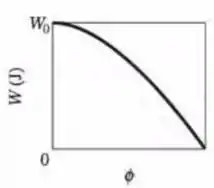
Uma força é aplicada a uma conta quando esta se move em linha reta, sofrendo um deslocamento de . O módulo de é mantido constante, mas o ângulo entre e o deslocamento da conta pode ser escolhido. A Fig. 7-23 mostra o trabalho realizado por sobre a conta para valores de dentro de um certo intervalo; . Qual é o trabalho realizado por se é igual a (a) e (b) ?
Passo 1
Esta é uma questão que envolve o trabalho de uma força constante. Para tanto, devemos nos lembrar que podemos calcular o trabalho de uma FORÇA CONSTANTE através da seguinte relação:
Onde é o ângulo entre os dois vetores.
Nesta questão ele nos dá um gráfico do trabalho realizado pela força em função do ângulo . Então, para determinar o trabalho que a força realiza quando o ângulo é igual a e , devemos primeiro determinar o valor de a partir do gráfico dado.
Passo 2
Vamos perceber que no gráfico, quando , o trabalho realizado pela força é . Então usando a relação dada no passo anterior, temos:
Isolando :
Lembrando que multiplicamos o deslocamento por um fator de para converter a unidade de para .
Passo 3
Com o valor de calculado, podemos usar a mesma relação para cada ângulo pedido no problema. Assim, para :
E para :
Resposta
- ;
- .