Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 10.9 - Ex. 52
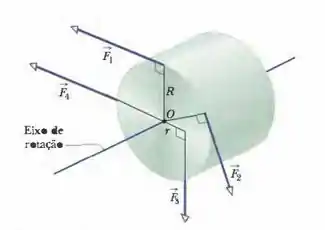
Na Fig. 10-39, um cilindro com uma massa de 2,0 kg pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: . As distâncias radiais são r = 5,0 cm e R = 12 cm. Determine: (a) o módulo; e (b) a orientação da aceleração angular do cilindro. (Durante a rotação, as forças mantêm os mesmos ângulos em relação ao cilindro).
Passo 1
Apesar de parecer complicado este exercício é bem tranquilo. Queremos a aceleração angular, dada por
Mas como?
Na figura acima, fica bem evidente que o torque nós conseguimos calcular, já temos o que precisamos na figura e no enunciado.
O que concluímos disso?
Que podemos usar uma equação que relaciona o torque e a aceleração. Qual?
Simples:
Devemos lembrar também que a relação é válida na forma vetorial:
O isso nos diz?
Que a direção do torque é igual a direção da aceleração angular! Isso já nos ajuda na letra b, ok?!
Passo 2
Para começar vamos calcular o torque resultante das 4 forças:
Vamos calcular um por um. E não se esqueçam de aplica a regra da mão direita!
Para a Força 1:
Para a Força 2:
Para a Força 3:
A linha de ação da força 4 passa direto pelo eixo de rotação, ou seja:
No torque total:
Passo 3
Agora precisamos achar o momento de inércia do cilindro em relação ao seu centro de massa.
Já sabemos como ele é calculado:
Substituindo:
Agora conseguimos achar a velocidade angular:
Então:
Como a aceleração tem a mesma direção do torque, olhando a face da frente do cilindro, ela está no sentido anti-horário (+).