Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 55
A componente do spin de um elétron é , mas a magnitude do vector de spin é . Qual é o ângulo entre o vetor de momento angular de spin e o eixo positivo?
Passo 1
Como a componente do spin é negativa, nós sabemos que ela aponta para baixo, no sentido do eixo negativo:
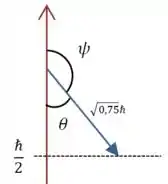
E o ângulo que queremos descobrir (entre o vetor e o sentido positivo do eixo ) é .
Passo 2
E agora vamos encontrar uma expressão para :
E então:
Resposta
O ângulo é de .
Exercícios de Livros Relacionados
O Big Ben (Fig. P10.17), relógio da torre do Parlamento em Londres, tem ponteiros de horas e minutos com comprimentos de 2,70m e 4,50m e massas de 60,0k g e 100k g , respectivamente. Calcule o momento
O vetor momento angular de um giroscópio de precessão varre um cone, conforme mostrado na Figura P10.58. A velocidade angular da ponta deste vetor, chamada frequência precessional, é dada por w p=τ /
Um skatista com seu skate pode ser modelado como uma partícula de massa 76,0k g , localizada em seu centro de massa, 0,500 m acima do chão. Como mostrado na Figura P10.84, o skatista parte do repouso
A figura abaixo mostra a variação com o tempo do torque τ que age sobre um disco inicialmente em repouso que pode girar como um carrossel em torno do centro. A escala do eixo τ é definida por τ s = 4
9.8E A hélice de um helicóptero contém três hastes, cada uma com um comprimento de 4,0m e massa 60kg . A hélice gira com velocidade de 10 giros por segundo. Supondo que a massa por unidade de comprime