Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.Problemas - Ex. 69
Um pequeno bloco com massa de está ligado a um fio que passa através de um buraco em uma superfície horizontal sem atrito. Inicialmente, o bloco gira a uma distância de do buraco com uma velocidade de . A seguir, o fio é puxado por baixo, fazendo o raio do círculo encurtar para . Nessa nova distância verifica-se que sua velocidade passa para 2,80 m/s.
a) Qual era a tensão no fio quando o bloco possuía velocidade v = 0,70 m/s?
b) Qual é a tensão no fio quando o bloco possuía velocidade final v = 2,80 m/s?
c) Qual foi o trabalho realizado pela pessoa que puxou o fio?
Passo 1
Opa, bora resolver esse problema! O enunciado dá pra a gente o seguinte esquema:
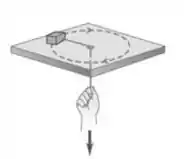
Esse quadradinho em cima da placa tem ele tá girando com um raio de e com uma velocidade de . Quando a gente começa a puxar o fio pra baixo o raio vai diminuindo. Quando o raio passa a ser a velocidade se torna igual a .
Ahh, aqui não temos atrito! Agora precisamos encontrar qual a tensão no fio. Para isso, vamos dar uma olhada no DCL desse movimento:
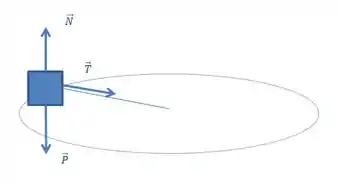
Repara só, que essa tração é a resultante que aponta para o centro do movimento, que também é chamada de Força Centrípeta, portanto, teremos que:
E a força centrípeta possui uma fórmula conhecida, que é dada por:
Sendo assim, conseguimos encontrar a nossa tração.
Passo 2
Encontrando a tração para a letra a), teremos:
Passo 3
Já para a letra b), temos que o raio foi diminuído ao se puxar a corda e diminuir sua extensão, agora temos um novo raio e uma nova velocidade.
E nossa tarefa aqui será encontrar a tração nessa nova trajetória, para isso, vamos usar as mesmas considerações que na letra a).
Passo 4
Para a letra c), queremos saber qual foi o trabalho realizado para fazer essa mudança, onde o raio da trajetória diminuiu e a velocidade aumentou.
Esse trabalho foi realizado pela força de tração, e sabemos que:
No entanto, essa tração varia ao longo do movimento, não conhecemos a trajetória que aconteceu enquanto o raio diminuía, não sabemos nada do movimento.
Mas podemos utilizar o teorema trabalho-energia, que nos diz que:
E nesse movimento, como a única força capaz de gerar trabalho é a tração (a força peso e a normal não irão gerar trabalho, pois são perpendiculares ao movimento), teremos:
E agora é só encontrar essa variação de energia cinética:
Substituindo os valores, teremos:
Ou seja, a pessoa que puxou o fio, realizou um trabalho de , através da força de tração para diminuir o raio dessa trajetória da forma que foi descrita no enunciado.Fechou!?
Resposta
O trabalho realizado pela pessoa ao puxar o fio é de: