Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 55

Você deve testar um carro e avaliar seu desempenho em relação às especificações forecidas. O motor deste carro tem a potência alegada de 164 hp. Este é um valor de pico, o que significa que ele é capaz, no máximo, de prover energia às rodas de tração à taxa de 164 hp. Você verifica que a massa do carro (incluindo o equipamento de teste e o motorista embarcados) é 1220 kg. Enquanto viajando com a rapidez constante de 55,0 mi/h, seu computador de bordo acusa que o motor está desenvolvendo 13,5 hp. Em experimentos prévios, foi verificado que o coeficiente de atrito de rolamento no carro é 0.0150. Suponha uma força de arraste sobre o carro variando com o quadrado da rapidez, isto é, F a = C v 2 . (a) Qual é o valor da constante C? (b) Considerando a potência de pico, qual é a rapidez máxima (com precisão de 1 mi/h) que você espera que o carro atinja? (Este problema pode ser resolvido à mão, analiticamente, mas ele pode ser resolvido mais facil e rapidamente usando urna calculadora gráfica ou urna planilha eletrônica.)

Passo 1

Letra (a)

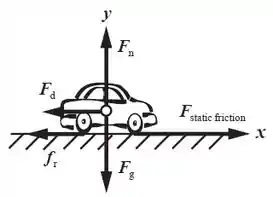
A potência é dada por:

P = F a t v             ( 1 )

Pela segunda lei de Newton em x:

F a t - f r - F d = 0

F a t = f r + F d

F a t = C v 2 + μ m g             ( 2 )

Jogando a (2) na (1):

P = C v 2 + μ m g v

P = C v 3 + μ m g v             ( 3 )

Passo 2

Isola o C:

C v 3 = P - μ m g v

C = P v 3 - μ m g v 2

Joga os valores:

C = 13,5   h p 55   m i / h 3 - 0,015 1220   k g 9,81 m s 2 55 m i h 2 = 0,381   m g / m

Passo 3

Letra (b)

Vamos pegar a equação (3) e reescrever na forma

C v 3 + μ m g v - P = 0

v 3 + μ m g C v - P C = 0

Jogando os valores, a gente tem:

v 3 + 471,4   m 2 / s 2 v - 3,2 × 10 5   m 3 / s 3 = 0

Resolvendo a equação cúbica em v (usando algum programa ou calculadora especial)

v = 148   m i / h

Resposta

Letra (a): C = 0,381   m g / m

Letra (b): v = 148   m i / h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco composto de diâmetro externo de 140,0c m é constituído de um disco maciço uniforme com raio de 50,0c m e densidade de área de 3,0g / c m 2 , cercado por um anel concêntrico com raio interno d
Um cilindro homogêneo com 10 cm de raio e uma massa de 20 kg está montado de modo a poder girar livremente em tomo de um eixo horizontal paralelo ao eixo central longitudinal do cilindro e situado a 5
a ) Mostre que as unidades de 0.5 I w ² ² são equivalentes às unidades de joule . Explique por que a unidade " rad” não precisa ser incluída nessas unidades b) Geralmente w é expresso em rev/min em ve
Um cilindro de massa M e raio R possui uma densidade cresce linearmente a partir do seu eixo, p = ar, onde aé uma constante positiva, a) Calcule o momento de inércia do cilindro relação a um eixo long
Exatamente uma volta de uma corda flexível de massa m é enrolada na periferia de um cilindro uniforme maciço de massa M e raio R . O cilindro gira sem atrito em tomo de um eixo horizontal ao longo do