Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 37
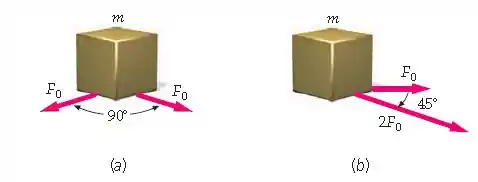
Uma força horizontal de magnitude causa uma aceleração de magnitude quando atuando sobre um objeto de massa que desliza sobre uma superfície sem atrito. Encontre a magnitude da aceleração do mesmo objeto nas circunstâncias mostradas nas Figuras 4-35a e 4-35b.
Passo 1
Olá, querido! Tá bem? Então, o que ele quer é a magnitude da aceleração resultante em cada caso desse. E a aceleração resultante é a que aparece na segunda lei de Newton:
Onde é a força resultante sobre o objeto e é a massa do objeto. Então a gente precisa achar para cada caso apresentado é a força resultante sobre o bloco. Então conseguimos achar .
Mas percebe que as forças atuando nas duas figuras estão em função de . Não temos uma expressão para . Só que podemos achar uma expressão para ela!
Como? Usando a segunda lei de Newron para o caso onde temos apenas a força sobre o objeto causando a aceleração . Nesse caso, só há , então a força resultante é . E como , podemos escrever:
Prontinho, agora a gente tem tudo para entrar nos itens e resolver. Bora lá!
Passo 2
a) Precisamos achar o módulo da força resultante para esse caso, que vai ser a soma vetorial das duas forças atuando no bloco. Podemos fazer o desenho dessas forças em um plano e desenhar a soma vetorial no formato de triângulo, assim:
Esse quadrado azul é o nosso bloco visto de cima.
Para esquematizar a soma vetorial a gente precisa preservar as orientações dos vetores, colocar os vetores que serão somados um começando no fim do outro, e colocar o vetor resultante começando no ínicio do primeiro vetor e terminando no final do último.
Aí para achar o tamanho do vetor a gente calcula o tamanho do segmento verdinho da nossa figura. Como a gente tem um triângulo retângulo, podemos usar Pitagoras:
Passo 3
A aceleração é então dada pela segunda lei de Newton:
Lembrando que :
Obs: Como ele só pede a magnitude, esse já é o resultado final. Mas se quiser saber a orientação de como está no gabarito, você pode perceber que o triângulo retângulo que a gente formou com as forças tem lados iguais. Ou seja, ele é a metade de um quadrado.
Então podemos enteder que faz com a horizontal. E assim, também.
Passo 4
b) Precisamos achar o módulo da força resultante para esse caso, que também vai ser a soma vetorial das duas forças atuando no bloco. Podemos fazer o desenho dessas forças em um plano e desenhar a soma vetorial no formato de triângulo, assim:
Esse quadrado azul é o nosso bloco visto de cima.
Esquematizamos a soma vetorial da mesma forma: a gente precisa preservar as orientações dos vetores, colocar os vetores que serão somados um começando no fim do outro, e colocar o vetor resultante começando no ínicio do primeiro vetor e terminando no final do último.
Aí para achar o tamanho do vetor a gente calcula o tamanho do segmento verdinho da nossa figura. Percebe que a gente pode descobrir o valor de . Como? Pela figura, ele e somam , então:
Então a gente tem dois segmentos de um triângulo e o ângulo entre eles, e quer saber o tamanho do segmento oposto. Isso é uma dica para achar usando a lei dos cossenos:
Passo 5
A aceleração é então dada pela segunda lei de Newton:
Lembrando que e :
Tirando da raiz:
Obs: Novamente, essa já pode ser sua resposta final. Mas se quiser achar a orientação de , você pode achar a orientação de usando a lei dos senos.
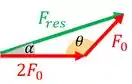
Como é oposto a , e é oposto a :